Understanding how to find a z critical value is an important step in statistics, especially when constructing confidence intervals or performing hypothesis tests. A z critical value shows the cutoff point on a standard normal distribution where results become statistically significant. In this post, you’ll learn a simple, step-by-step method to find z score critical values manually using a Z table. You’ll also see examples for left-tailed, right-tailed, and two-tailed tests to help you understand the process clearly.
What is a Z Critical Value?
A z critical value is a point on the standard normal distribution that separates the rejection region from the acceptance region. In simple terms, it gives the cut-off value beyond which results count as statistically significant. During a hypothesis test, you compare the computed z test statistic with the z critical value to decide whether to reject the null hypothesis. You also use z critical values when calculating confidence intervals for the mean, especially when the population standard deviation is known. By setting this clear threshold, z critical values play a central role in statistical decision-making.
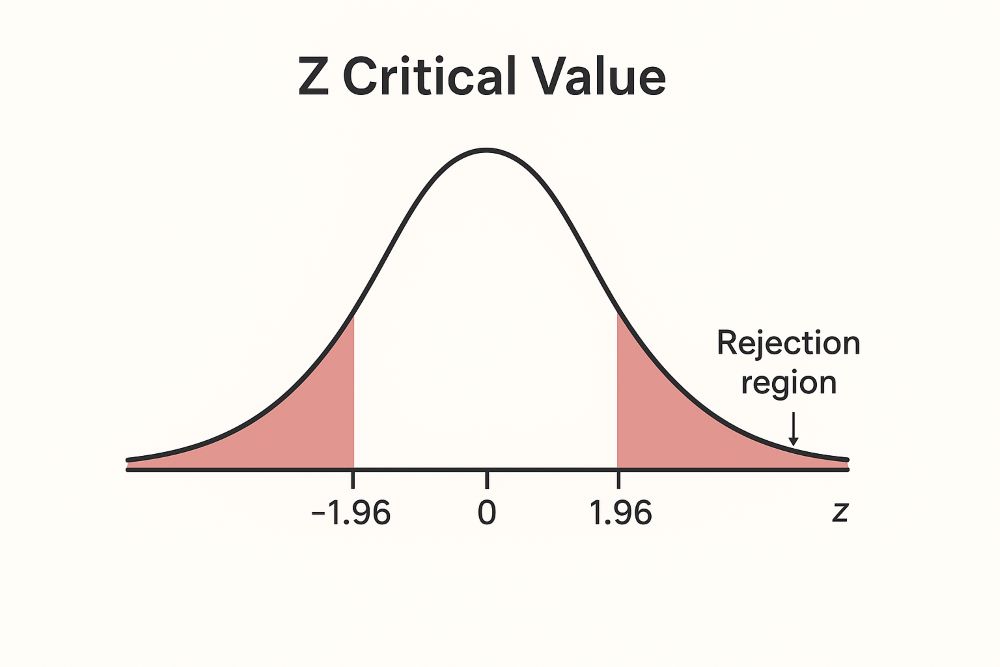
The standard normal distribution is a bell-shaped curve with a mean of zero and a standard deviation of one. Each z critical value corresponds to a probability, or alpha level, which shows the risk of making a Type I error. For example, at a 5% significance level in a two-tailed test, the cutoff is ±1.96. The figure below shows this threshold on the curve, with the shaded rejection regions.
The z critical value formula is defined as follows:
$$Z_{\alpha} = \Phi^{-1}(1 – \alpha)$$
Where:
- $\Phi^{-1}$ is the inverse of the cumulative distribution function (CDF) of the standard normal distribution. In other words, it is the function that tells us the z score that corresponds to a given probability
- α is the significance level. It represents the probability of rejecting the null hypothesis when it is actually true.
Therefore, for a one-tailed test, the entire alpha level is placed in a single tail of the distribution. This means you directly apply the formula without changing the α. However, for a two-tailed test, the alpha level is divided equally between the two tails. In this case, you replace α in the formula with α/2, since each side of the distribution contains half of the rejection area.
Steps to Compute Z Critical Value Manually From Z tables
Step 1: Identify the Confidence Level or Significance Level
The first step in finding a z critical value is to determine your confidence level or the significance level (α). These two values are related, and knowing one allows you to calculate the other. Most statistical tests use common confidence levels such as 90%, 95%, or 99%. Follow the steps below to make this process easy and clear:
- Step 1: Write down your confidence level (for example, 95%).
- Step 2: Convert the percentage to a decimal by dividing by 100 (95% → 0.95).
- Step 3: Find the significance level using the formula:
α=1−confidence level - Step 4: Substitute the value. For example, if the confidence level is 0.95, then
α=1−0.95=0.05.
Understanding this relationship between confidence level and significance level is important because it forms the basis for finding the correct z critical value in the next step.
Step 2: Determine the Type of Test
After identifying your significance level, the next step is to determine the type of test you are working with. This is important because the type of test affects where the rejection region lies on the standard normal distribution curve. In hypothesis testing, there are three main types of tests:
- Left-tailed test: The critical region is in the left tail of the distribution. This means you are looking for a negative z critical value.
- Right-tailed test: The critical region is in the right tail. Thus, the z critical value will be positive.
- Two-tailed test: The significance level (α) is divided equally between both tails. This implies that each tail will be α/2.
Step 3: Find Z Critical Value Using a Z Table
The traditional way to find a z critical value is by using a Z table. This table shows the cumulative probability or area under the standard normal curve up to a specific z value. Thus, depending on your type of test, you can use either a positive Z table or a negative Z table. Specifically, you should:
- Use a positive Z table when finding right-tailed or two-tailed z critical values. It gives the area from the far left up to a positive z value.
- Use a negative Z table when finding left-tailed z critical values. It gives the area to the left of a negative z value.
However, if you only have a positive Z table, you can still find left-tailed probabilities by using the symmetry of the normal distribution. In this case, you apply this formula:
P(Z<−z)=1−P(Z<z)
In summary, to find a z critical value from the standard normal table, you only need to follow these simple steps:
- Identify the significance level (α) from your previous step.
- Determine the type of test (i.e. left-tailed, right-tailed, or two-tailed).
- Calculate the cumulative probability based on your test type.
- Locate that probability in the appropriate Z table (positive or negative) and find the corresponding z value.
Finding Z Critical Values Using Z Tables: Worked Examples
Now that you understand how to use Z tables, let’s go through clear examples for each type of test. These examples will help you see exactly how to find the z critical value manually using either a positive or negative Z table.
Example 1: Left-Tailed Test
A left-tailed test checks for extreme values in the lower tail of the distribution. Suppose that the significance level, α=0.05. This is a one-sided (left-tailed) test. Thus, to find the critical value, follow these steps:
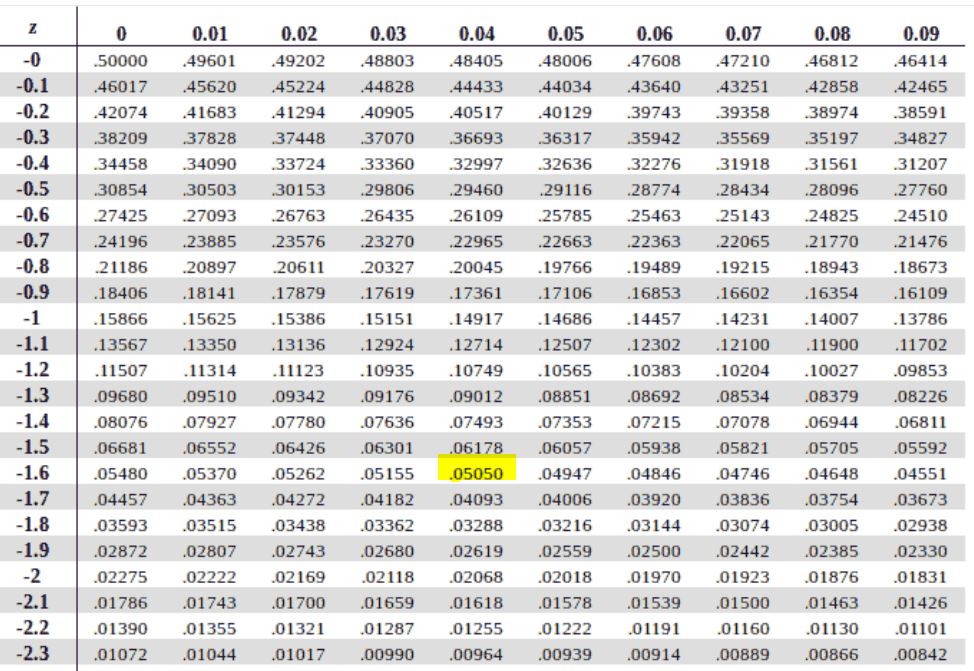
- Using the negative z table, look for a z score value corresponding to p = 0.05.
- From the negative z table, the z value corresponding to p = 0.05 is -1.64 as shown below:
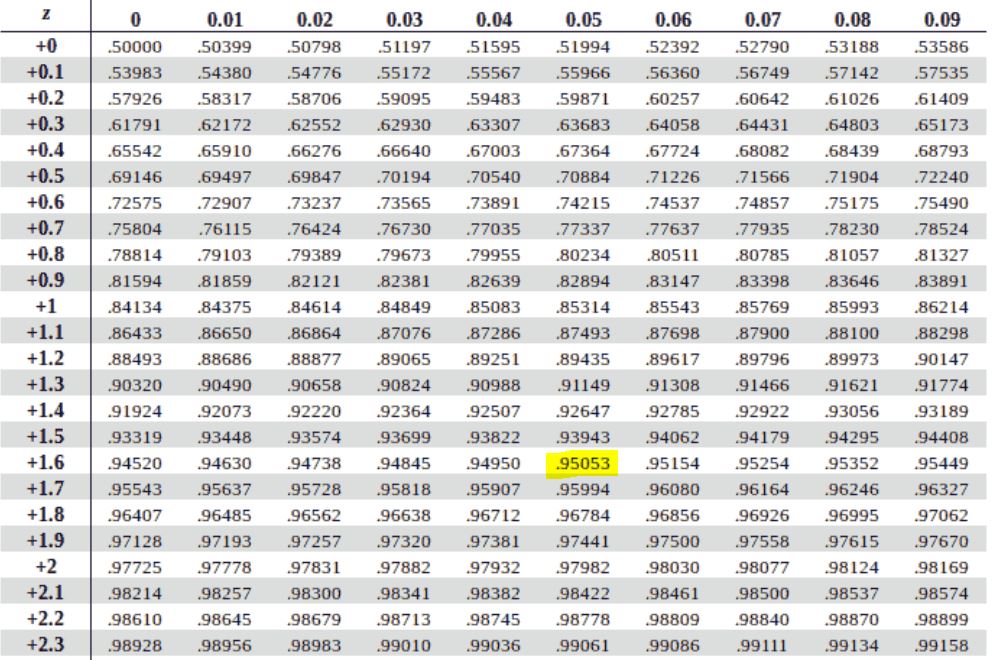
- However, if using the positive z table, use the symmetry formula:
- 1-0.05 = 0.95
- Next, find 0.95 in the positive table and assign a negative sign. This gives -1.65, as shown below.
Example 2: Right-Tailed Test
A right-tailed test checks for extreme values in the upper tail. In this case, you need to find a critical value to the right of the standard normal curve. Suppose the significance level is α=0.05. To find the right-sided z critical value, you need to find the cumulative area to the left of the critical value, 1-α = 1-0.05 = 0.95. Next, look up 0.95 in the positive z table. The corresponding z value is 1.65 as shown below:

Example 3: Two-Tailed Test
For a two-tailed test, you need to divide the significance level, α equally between both tails of the curve. Let’s assume that the significance level, α=0.05, to find the critical value, follow these steps:
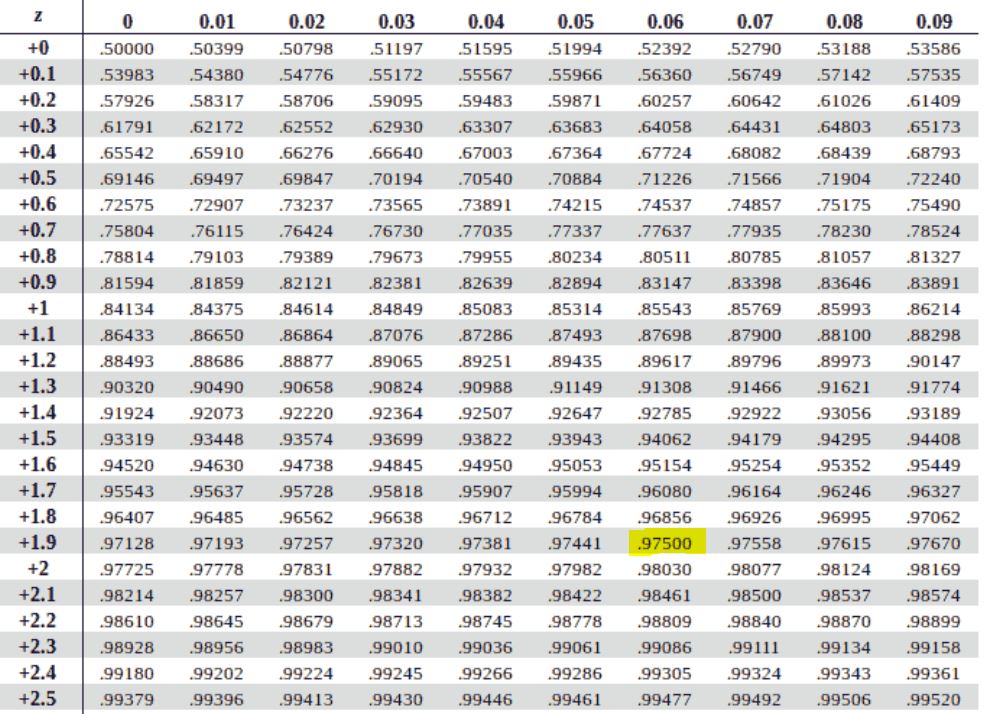
- Divide α by 2 for both tails:
α/2=0.05/2 = 0.025 - For the right tail, find the cumulative area:
1−0.025=0.975 - Look up 0.975 in the positive Z table.
- The z critical values are therefore ±1.96 (one positive, one negative), as shown below.
Want to skip the manual lookup? Try our free Z Critical Value Calculator to automatically calculate z-critical value by simply entering significance level (α) and the type of test. The calculator provides accurate critical value from z table, along with a step-by-step explanation to help you understand how the critical value was obtained.
Commonly Used Z Critical Values for Confidence Levels
Before you calculate your own value, it’s helpful to know some commonly used z critical values. These values are used often in statistics for confidence intervals and hypothesis tests. The table below shows the confidence level, significance level (α), and the corresponding z critical value for two-tailed tests.
| Confidence Level | Significance Level (α) | Tail Type | Area in Each Tail (α/2) | Z Critical Value |
|---|---|---|---|---|
| 80% | 0.20 | Two-tailed | 0.10 | ±1.282 |
| 85% | 0.15 | Two-tailed | 0.075 | ±1.440 |
| 90% | 0.10 | Two-tailed | 0.05 | ±1.645 |
| 92% | 0.08 | Two-tailed | 0.04 | ±1.751 |
| 95% | 0.05 | Two-tailed | 0.025 | ±1.960 |
| 96% | 0.04 | Two-tailed | 0.02 | ±2.054 |
| 97% | 0.03 | Two-tailed | 0.015 | ±2.170 |
| 98% | 0.02 | Two-tailed | 0.01 | ±2.326 |
| 99% | 0.01 | Two-tailed | 0.005 | ±2.576 |
| 99.9% | 0.001 | Two-tailed | 0.0005 | ±3.291 |
💡 Tip: Use the positive value for right-tailed tests and the negative value for left-tailed tests. For example, if your test is left-tailed at α = 0.05, use z = -1.645.
Conclusion
Finding a z critical value becomes easy when you follow the right steps. First, identify your confidence level, then determine the type of test, and finally look up the value in a Z table or use an online calculator. While the manual method helps you understand the concept, using a Z Critical Value Calculator is faster and more accurate. It gives you the correct value instantly and explains each step clearly.
Frequently Asked Questions
A Z critical value is the point on the standard normal distribution that marks the boundary for rejecting or not rejecting the null hypothesis. It represents how many standard deviations away from the mean a certain confidence or significance level lies.
To find the Z critical value from a confidence level, subtract the confidence level from 1 to get the significance level (α). Then, divide α by 2 for a two-tailed test. Finally, find the cumulative probability (1 − α/2) in the Z table or use a Z critical value calculator to get the exact value.
For a 95% confidence level, the significance level (α) is 0.05. Dividing by 2 gives 0.025 for each tail, and the cumulative probability is 0.975. The corresponding Z critical value is ±1.96.
– Left-tailed tests use a negative z value (area in the left tail).
– Right-tailed tests use a positive z value (area in the right tail).
– Two-tailed tests split α between both tails, using both the positive and negative critical values.
Yes. You can use an online Z critical value calculator, which gives the result instantly. It only requires you to select your confidence level or significance level and the test type. It’s a faster and more accurate way compared to manual lookup.
Some of the most common Z critical values include:
– 90% confidence → ±1.645
– 95% confidence → ±1.96
– 99% confidence → ±2.576
These are often used for hypothesis testing and confidence intervals in research and data analysis.
