Use this binomial distribution calculator to quickly compute exact probabilities, cumulative probabilities, and the binomial probability mass function (PMF) table. You only need to insert the number of trials (n), the probability of success (p), and the number of successes (x). For example, entering 10 trials, 0.8 probability of success, and 6 successes instantly gives you P(X = 6), P(X < 6), P(X ≤ 6), P(X > 6), and P(X ≥ 6). The calculator also displays the mean, standard deviation, and a full PMF table showing P(X = k) for all possible outcomes.
What is a Binomial Distribution Calculator?
A binomial distribution calculator also known as the binomial probability calculator is a simple online tool that helps you compute exact and cumulative probabilities of getting a specific number of successes in a fixed number of independent trials. It use the binomial distribution formula to instantly calculate probabilities such as P(X = x), P(X < x), P(X ≤ x), P(X > x), and P(X ≥ x) based on the number of trials (n), the probability of success (p), and the number of successes (x).
Therefore, instead of solving binomial probabilities using complex formulas and binomial tables by hand, the calculator gives you accurate results with a click of a button. Besides the probabilities, it also provides the distribution mean and standard deviation, and a full probability table for all values of k. This makes it ideal for students, teachers, researchers, and anyone who regularly works with binomial distributions.
How to Use Our Binomial Distribution Calculator
Our binomial probability calculator is easy to use. Follow these simple steps:
- Enter the number of trials (n).
- Enter the probability of success (p).
- Enter the number of successes (x).
- Click the “Calculate” button.
Once you click the button, the calculator will instantly show:
- P(X = x)
- Cumulative probabilities such as P(X < x), P(X ≤ x), P(X ≥ x), and P(X > x)
- The mean and standard deviation of the binomial distribution
- A full probability table showing P(X = k) for all possible values of k
Binomial Distribution Formula
The binomial distribution formula helps you calculate the probability of getting exactly x successes in n independent trials, each with a probability of success p. Our binomial probability calculator uses the formula:
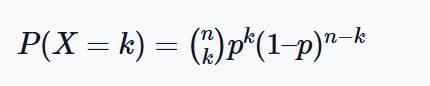
Where:
- n is the total number of trials
- k is the number of successes
- p is the probability of success in a single trial
- (1 – p) is the probability of failure in a single trial
This formula shows how likely it is to observe a specific number of successes under a binomial setting. If you want a deeper explanation, step-by-step examples, and common applications, read our full guide to the binomial distribution.
How to Compute Binomial Probabilities using the Calculator [With Example]
To help you understand how the tool works, here are a few example calculations using the Binomial distribution Calculator. These examples show how the calculator applies your inputs to generate exact and cumulative probabilities.
Scenario: A manufacturer knows that 3% of its bulbs are defective. An inspector tests 20 bulbs. Let X be the number of defective bulbs. The calculator automatically displays all exact and cumulative probabilities for this setup. The sections below show how to interpret each value from the results.
1) Finding Exact Probability, P(X=k)
i) From the scenario, what is the probability that exactly 2 bulbs are defective?
Solution
To find the probability of getting exactly 2 defective bulbs, follow these steps:
- Enter the number of trials (n) = 20
- Enter the probability of success (p) = 0.03
- Enter x = 2
- Look for P(X = 2) in the calculator results
From the calculator output, P(X = 2) = 0.0988 (See Figure 1). This means there is about a 9.88% chance of finding exactly 2 defective bulbs.
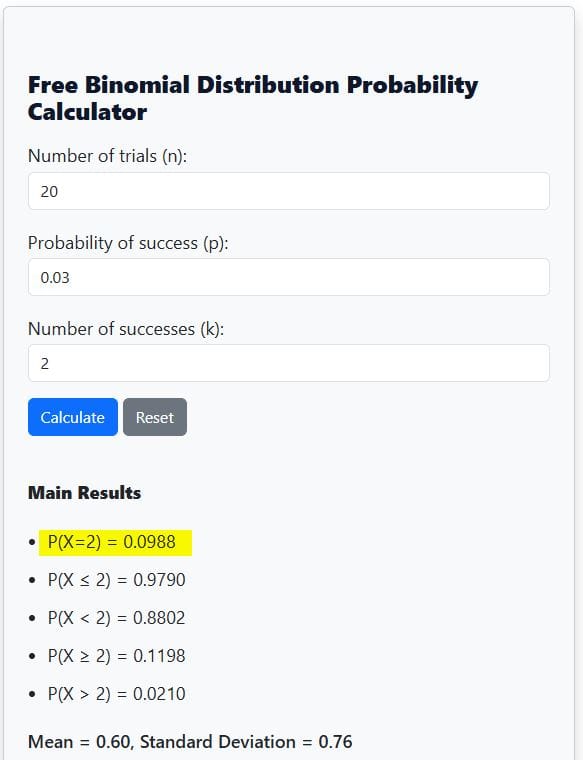
2) Finding Cumulative Probability, P(X≤k)
ii) From the scenario, what is the probability that at most 2 bulbs are defective?
Solution
To find the probability that at most 2 defective bulbs are found (0, 1, or 2), follow these steps:
- Enter the number of trials (n) = 20
- Enter the probability of success (p) = 0.03
- Enter x = 2
- Look for P(X ≤ 2) in the calculator results.
From the calculator output, P(X ≤ 2) = 0.9790 (See Figure 2). This implies that there is a 97.9% chance that the inspector finds at most 2 defective bulbs.
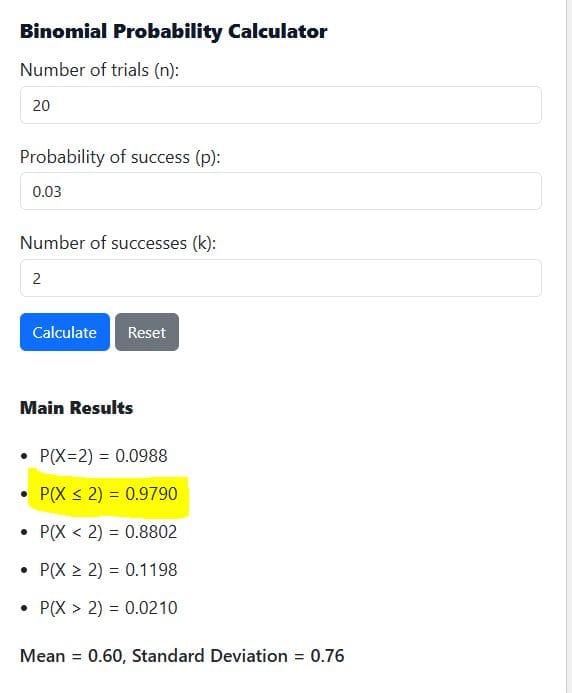
3) Find Cumulative Probability, P(X<k)
iii) From the scenario, what is the probability that less than 2 bulbs are defective?
Solution
To find the probability that the inspector finds fewer than 2 defective bulbs (either 0 or 1), follow these steps:
- Enter the number of trials (n) = 20
- Enter the probability of success (p) = 0.03
- Enter x = 2
- Look for P(X < 2) in the calculator results
From the calculator output, P(X < 2) = 0.8802 (See Figure 3). This means that there is an 88.02% chance of finding fewer than 2 defective bulbs.
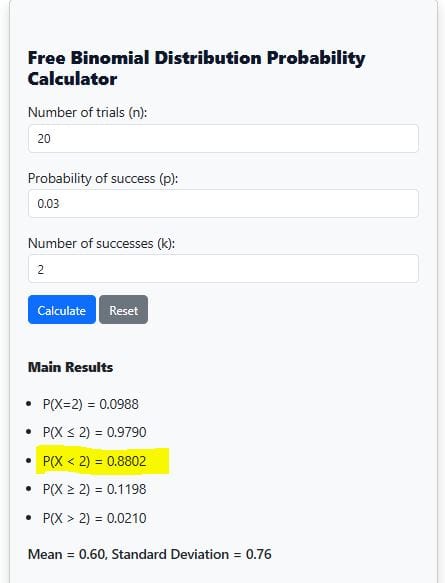
4) Find Cumulative Probability, P(X≥k)
iv) From the scenario, what is the probability that at least 3 bulbs are defective?
Solution
To find the probability of getting 3 or more defective bulbs, follow these steps:
- Enter the number of trials (n) = 20
- Enter the probability of success (p) = 0.03
- Enter x = 3
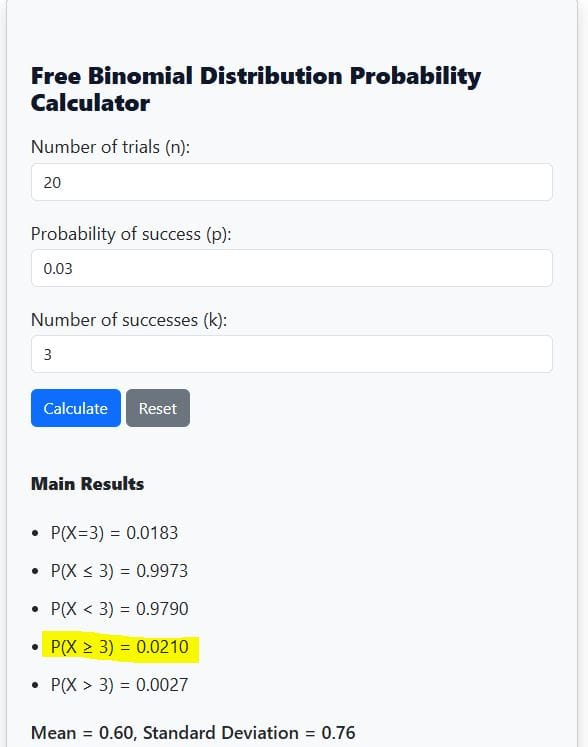
- Look for P(X ≥ 3) in the calculator results
From the calculator output, P(X ≥ 3) = 0.0210 (See Figure 4). This suggests that there is about a 2.10% chance of finding 3 or more defective bulbs in the sample.
5) Find Cumulative Probability, P(X>k)
v) From the scenario, what is the probability that greater than 1 bulbs is defective?
To find the probability of getting one or more defective bulbs, follow these steps:
- Enter the number of trials (n) = 20
- Enter the probability of success (p) = 0.03
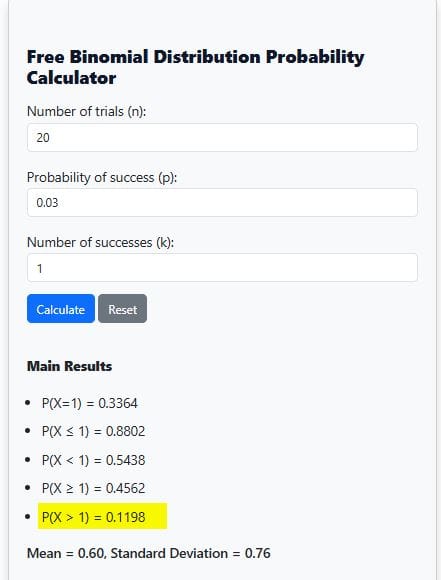
- Enter x = 1
- Look for P(X > 1) in the calculator results
From the calculator output, P(X > 1) = 0.1198 (See Figure 5). This suggests that there is about a 11.98% chance of finding one or more defective bulbs in the sample.
Related Articles
- How to calculate binomial probabilities manually
- Understanding the mean of binomial distribution
- Understanding the variance of binomial distribution
Frequently Asked Questions
A binomial probability calculator helps you find the probability of getting a certain number of successes in a fixed number of trials. You only enter the number of trials, the probability of success, and the value of X.
Enter the number of trials, the probability of success, and the value of X. The calculator will show exact probabilities and cumulative probabilities like P(X = k), P(X ≤ k), P(X < k), P(X ≥ k), and P(X > k).
You can use it to solve probability questions in quality control, surveys, genetics, reliability testing, and any situation with a fixed number of independent trials.
Yes. It displays all results at once, including exact probability and cumulative probabilities. You do not have to choose them separately.
No. The calculator is easy to use. You only enter three inputs, and it does the math for you.
Yes. The calculator uses the standard binomial formula to compute probabilities. It gives accurate results for all valid inputs.