This calculator helps you determine the minimum sample size for your study or survey using Cochran’s formula. It automatically applies the appropriate formula based on your input:
- For an unknown or infinitely large population, the calculator uses the standard Cochran’s formula for infinite populations.
- For a finite and known population, it applies the finite population correction (FPC) to compute the adjusted sample size.
In addition to providing the minimum sample size, the calculator also gives a step-by-step solution of how the sample size was calculated, making it easy to understand and apply for your research.
How to Determine Sample Size Using the Cochran’s Calculator
Determining the required sample size for your study using this cochran’s formula calculator is simple & straightforward. Just follow these simple steps:
- Enter your confidence level (%): This represents how certain you want to be that your sample accurately reflects the population. Common values are 90%, 95%, or 99%.
- Enter your margin of error (e): This indicates how much error you are willing to tolerate in your results. You only need to enter this value as a decimal. For instance, for 5% margin of error, you need to enter 0.05.
- Enter your estimated proportion (p): This is your best estimate of the population proportion. If you are unsure, use 0.5 (50%) to ensure the maximum sample size and the most conservative estimate.
- Enter the population size (N) (optional): If you know your total population, enter it here. If not, you can leave it blank. The calculator will assume an infinite population.
- Click “Calculate” button: The calculator instantly computes your required sample size using Cochran’s formula.
Note. On hitting the “Calculate” button, the calculator will provide you with the correct estimate for the sample size, along with easy-to-follow explanation. This will help you gain a comprehensive understanding of the logic behind the cochran’s formula.
Examples
Example 1. Let’s say you want to determine the sample size for a survey with the following conditions:
- Confidence level = 95% (Z = 1.96).
- Proportion (p) = 0.5
- Margin of error (e) = 0.05
To compute the sample size using the calculator, follow these steps:
- Insert 95 in the confidence level input section
- Insert margin of error 0.05
- Specify the proportion as 0.5
- Click the Calculate button
The calculator will give you the minimum sample size after rounding up as 385 (Figure 1).
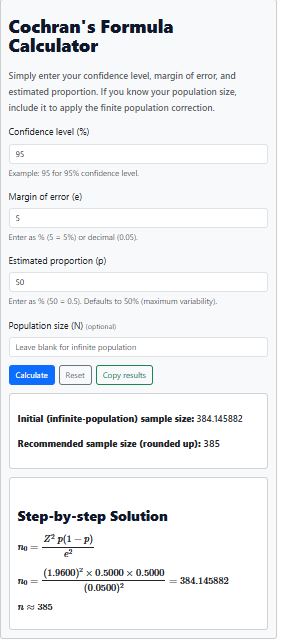
Example 2. Assuming the parameters remain the same as in example 1 (i.e. 95% confidence, p = 0.5, margin of error = 5%). Suppose now that the actual population size is known to be 1,000 people.
The calculator can adjust for the finite population correction for you. You simply need to specify the known population in the “Population size (N) (optional)” section and click the Calculate button.
The calculator will calculate and round up the adjusted sample size for you. The resulting sample size for 1000 people will be 278 participants (Figure 2).
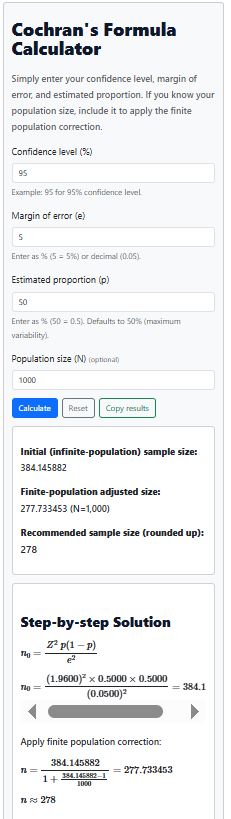
About the Cochran’s Formula
Cochran’s formula is a standard method for calculating the minimum sample size for a survey or study. It helps ensure your results are reliable and statistically valid.
For studies with a finite population, an adjustment called the finite population correction (FPC) is applied to avoid overestimating the required sample size.
For a detailed explanation of the formulas and how they work, see our full guide on Cochran’s Formula.