Poisson Distribution Calculator
The Poisson Distribution Calculator is a free tool that helps you quickly solve problems involving the Poisson probability distribution. The Poisson distribution is used to model the number of events that happen in a fixed time or space, given a known average rate. While the formula is straightforward, manual calculation can be tedious because it involves factorials and exponential terms. That’s why we created the Poisson Probability Calculator to help you saves time and reduce errors. With our poisson calculator, you can compute exact probabilities like P(X=k), cumulative probabilities such as P(X≤k), P(X<k), P(X>k), P(X≥k), and interval probabilities (P(a≤X≤b)) instantly. Besides, the calculator allows users to see the steps followed to compute any poisson probability. This makes it the best for beginners looking for to gain comprehensive understanding of poisson probabilities.
- Enter mean rate
- Select Probability Type from dropdown
- Enter k (number of events) or range (a, b)
- Click Calculate to get results
- Optional: Show Steps for step-by-step solution
How to Use Our Poisson Distribution Calculator
Tired of struggling with complex formulas or flipping through Poisson tables? Our Poisson Probability Calculator makes the process quick, accurate, and beginner-friendly. All you need to do is enter your values (mean, λ, and required probability, k), select the type of probability you want, and let the calculator handle the rest.
Here’s how it works:
- Enter λ (mean rate): Type in the average number of events that occur in a fixed interval.
- Enter k (number of events): Specify the exact number of occurrences, or provide values for a and b if you want an interval probability.
- Select probability type: Choose from the drop-down menu (Exact, Cumulative, or Interval).
- Click Calculate: Instantly get results for the probability, along with mean and standard deviation.
- Optional – Show Steps: Click the “Show Steps” button to see the detailed solution and learn how the probability was calculated.
Poisson Distribution & Formula
The Poisson distribution is a discrete probability distribution that expresses the likelihood of a given number of events occurring within a fixed interval of time, distance, or space, provided that these events occur with a known constant mean rate and independently of each other. It is commonly used in fields such as statistics, engineering, business, and the natural sciences to model rare events.
The Poisson probability formula is expressed as:
$$P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}$$
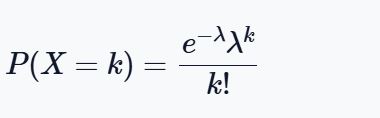
Where:
- P(X=k) is the probability of exactly k events occurring
- k is the number of occurrences (0, 1, 2, …)
- λ is the average rate of occurrence (mean number of events in the interval)
- e is mathematical constant (exponential), approximately 2.71828
- k! is the factorial of k
In addition to exact probabilities, cumulative probabilities can also be derived. These include:
- P(X≤k): probability that the number of events is less than or equal to k.
- P(X<k): probability that the number of events is less than k.
- P(X≥k): probability that the number of events is greater than or equal to k.
- P(X>k): probability that the number of events is greater than k.
- P(a≤X≤b): probability that the number of events falls within a specific range.
Note: The Poisson distribution has a unique property where the mean and variance are equal to λ.
When to Use the Poisson Distribution
The Poisson distribution is widely applied in situations where events occur independently and at a constant average rate within a fixed interval of time, distance, or space. It is especially useful when modeling rare or count-based events. Common applications of Poisson distribution include:
- Call center arrivals: Estimating the number of incoming calls within an hour.
- Website traffic events: Modeling clicks, logins, or form submissions per minute.
- Defects per batch in manufacturing: Predicting the number of faulty products in a given production run.
- Natural events: Measuring occurrences of earthquakes, accidents, or floods over a specified period.
Examples of Poisson Probability Problems
To better understand how the Poisson distribution works, let’s go through a few real-world examples. These Poisson probability examples show how the formula is applied and how our calculator can quickly provide the results.
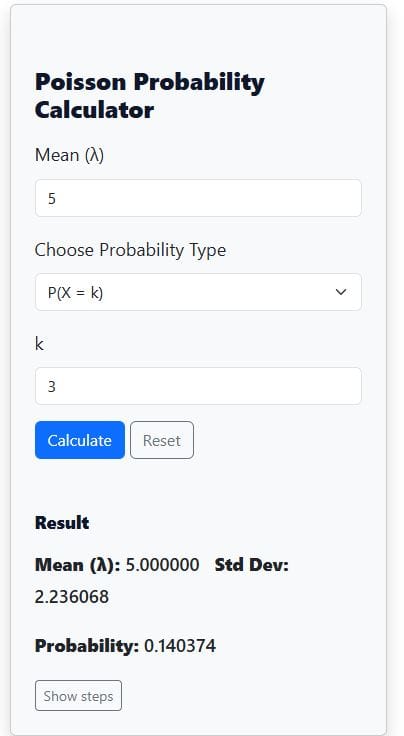
Example 1. Exact Poisson Probability
A hospital records an average of 5 emergency arrivals per night. What is the probability that exactly 3 patients will arrive tonight?
Solution
Based on the question, the mean rate, λ = 5.
We need to find P(X=3). This means that k = 3.
By definition, $$P(X=k) = \frac{e^{-\lambda}\lambda^k}{k!}$$
Subtituting the given values, we have:
$$ P(X=3) = \frac{e^{-5} \cdot 5^3}{3!}$$
Now, simplifying, we have:
$$P(X=3) =\frac{e^{-5} \cdot 125}{6}$$
=0.1404
Thus, there is about a 14% chance that exactly three patients will arrive tonight.
Now, using our binomial distribution calculator, we only need to insert the numbers and hit the calculate button. The results are as shown below:
Once you click show steps, you’ll see step-by-step solutions as shown below:
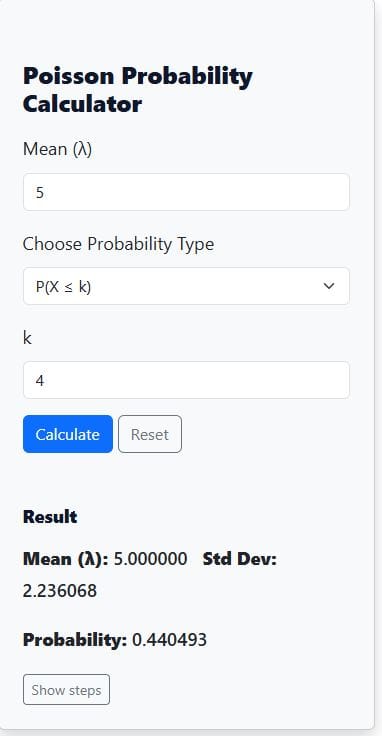
Example 2. Cumulative Poisson Probability
An online shop averages 5 customer orders every hour. What is the probability that 4 or fewer orders will be placed in the next hour?
Solution
Based on the question, the mean rate, λ=5.
We need to find P(X≤4).
By definition, P(X≤4)=P(X=0)+P(X=1)+P(X=2)
+P(X=3)+P(X=4)
Substituting the formula: $$P(X=k) = \frac{e^{-5} \cdot 5^k}{k!}$$
Now, simplifying step by step:
- $$P(X=0) = \frac{e^{-5} \cdot 5^0}{0!} \approx 0.0067$$
- $$P(X=1) = \frac{e^{-5} \cdot 5^1}{1!} \approx 0.0337$$
- $$P(X=2) = \frac{e^{-5} \cdot 5^2}{2!} \approx 0.0842$$
- $$P(X=3) = \frac{e^{-5} \cdot 5^3}{3!} \approx 0.1404$$
- $$P(X=4) = \frac{e^{-5} \cdot 5^4}{4!} \approx 0.1755$$
Adding them together, we have:
$$
P(X\le 4)\approx 0.0067+0.0337+0.0842 +0.1404+0.1755
$$
=0.4405
Thus, there is about a 44.05% chance that 4 or fewer orders will be placed in the next hour.
Now, using our Cumulative Poisson Probability Calculator, you only need to enter the values and hit calculate. The results are as shown below:
However, if you need to see the step-by-step solution, just click the show steps button. The results will be as shown below:
Frequently Asked Questions
A Poisson Distribution Calculator is an online tool that computes the probability of a certain number of events happening within a fixed interval. It can calculate exact probabilities, cumulative probabilities, and interval probabilities, along with the mean and standard deviation.
To calculate Poisson probability online, enter the mean rate (λ), specify the number of events k (or a range for interval probability), select the probability type from the drop-down, and click calculate. The tool instantly gives the probability value and step-by-step solution.
The calculator uses the Poisson probability formula:
$$P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!}$$
where:
– λ is the mean rate, and k
– k is the number of events.
The three conditions for using a Poisson distribution are:
– Events occur independently of each other.
– The average rate (λ) of events is constant over time or space.
– Two or more events cannot occur at exactly the same instant (only one event at a time is possible).
Yes. The calculator can find cumulative probabilities such as P(X≥k), or P(X<k), as well as probabilities within a range like P(a≤X≤b).
The Poisson distribution is commonly applied in scenarios such as predicting customer arrivals at a store, the number of website visits per hour, machine breakdowns in a factory, or the number of natural events like earthquakes in a year.