Determining the right sample size is one of the most important steps in any research design. It helps ensure that the results you get truly represent the whole population without wasting time or resources. Sample size determination simply means finding out how many people or items you need to include in your study to get reliable results. Researchers often use easy-to-apply Cochran’s, Slovin’s, and Taro Yamane’s formulas to calculate sample size accurately. In this guide, we’ll explain how each of these formulas works, when to use them, and show you step-by-step example showing how to calculate sample size.
Common Sample Size Calculation Formulas
Choosing the right formula for sample size calculation can feel confusing, especially when you’re not sure which one fits your study design. The good news is that researchers don’t have to start from scratch. There are a few tried-and-tested formulas that make the process simple and accurate. The three most widely used are Cochran’s Formula, Slovin’s Formula, and Taro Yamane’s Formula. Each of these formulas helps determine how many participants or observations you need based on your population size, confidence level, and margin of error. Let’s look at each one in detail and see when to use it.
1. Cochran’s Sample Size Formula
Cochran’s formula is best used for large or infinite populations, especially when estimating proportions in surveys. It assumes a normal distribution and requires a confidence level, margin of error, and estimated population proportion.
The cochran’s sample size formula is defined as follows:
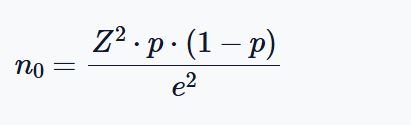
Where:
- n₀ is the required sample size
- Z is the Z-score for your desired confidence level (e.g., 1.96 for 95%)
- p is the estimated proportion of the population (use 0.5 if unknown)
- e is the desired margin of error
However, if your population is not very large (and is known), you can adjust the sample size using the finite population correction (FPC), as follows:
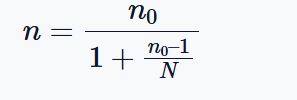
Where:
- $n_0$ is the sample size from the cochran’s formula for infinite population
- N is the known population size
- n is the estimated and adjusted sample size
Note. Cochran’s formula gives a statistically sound estimate and is preferred for academic and professional surveys.
Cochran’s Formula Examples
When the Population Is Very Large or Unknown
Scenario 1. Suppose you are conducting a nationwide survey to estimate how many people support a new education policy. The population is extremely large and unknown. You decide to use a 95% confidence level, a 5% margin of error, and assume maximum variability (p = 0.5).
To compute the sample size, you need to apply the cochran’s sample size formula, without adjusting for finite population correction, as follows:
The Cochran’s Formula is:
$n_0 = \frac{Z^2 \cdot p(1-p)}{e^2}$
Substituting the values, we have:
$n_0 = \frac{1.96^2 \times 0.5(1-0.5)}{0.05^2}$
Compute the values:
$n_0 = \frac{3.8416 \times 0.25}{0.0025}$
$ = \frac{0.9604}{0.0025}$
= 384.16
Rounding up to the nearest whole number, we have:
$n_0 = 385$
Thus, the required sample size is approximately 385 respondents.
When the Population Is Finite and Known
Scenario 2: Now imagine your study targets employees in a company with 10,000 staff members. You’ll use the same parameters: 95% confidence, 5% margin of error, and p = 0.5 but adjust for the finite population correction as follows:
The finite population correction formula is:
$n = \frac{n_0}{1 + \frac{n_0 – 1}{N}}$
In this scenario, we are assuming all the parameters in scenario 1 remain the same. That is, p = 0.5, margin of error is 5% and 95% confidence level.
Recall, without using the finite population correction, the sample size is 384.16
Now, substituting the values, we have:
$n = \frac{384.16}{1 + \frac{384.16 – 1}{10,000}}$
Solving the above equation, gives:
$n = \frac{384.16}{1 + 0.0383}$
$= \frac{384.16}{1.0383}$
$n = 369.98$
Rounding up to the nearest whole number, we have:
n = 370
Thus, the corrected sample size for a finite population of 10,000 is approximately 370 respondents.
Struggling with Cochran’s formula? Our Cochran’s Sample Size Calculator computes the correct sample size and provides a clear, step-by-step solution for every scenario.
2. Slovin’s Sample Size Formula
Slovin’s formula is a simpler and quicker approach when you know your total population size but don’t have information about its variability. It’s widely used in business, education, and social science research for general surveys.
The Slovin’s formula is given by:
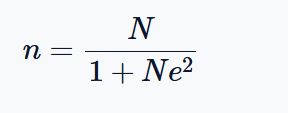
Where:
- n is the minimum sample size
- N is the total population size
- e is the approximated margin of error
Although it’s not based on strict statistical theory like Cochran’s, Slovin’s formula provides a reasonable estimate when researchers only need a general idea of sample size.
Slovin’s Formula Sample Size Determination Example
Imagine you’re conducting a survey among college students in a university with 5,000 students. You don’t have information about how opinions vary among students, so you decide to use Slovin’s Formula to determine a suitable sample size. Assuming the margin of error (e) is 5%, you can compute the required sample size as follows:
By definition, the Slovin’s formula is given by:
$n = \frac{N}{1 + N e^2}$
Substituting the values, we have:
$n = \frac{5000}{1 + 5000(0.05)^2}$
Next, compute the sample size as follows:
$n = \frac{5000}{1 + 5000(0.0025)}$
$n = \frac{5000}{1 + 12.5}$
$= \frac{5000}{13.5}$
$n= 370.37$
Rounding up to the nearest whole number, we have 371
Hence, the required sample size is approximately 371 respondents.
Need a quick way to find your sample size? Try our Slovin’s Sample Size Calculator. It instantly computes the correct sample size and shows a step-by-step breakdown of the entire calculation
💡 Tip: The Slovin’s Formula is perfect when you only know the population size and want a quick way to estimate your sample without complex statistical assumptions.
3. Taro Yamane’s Formula
The Taro Yamane sample size formula is one of the simplest and most widely used methods for determining sample size when the population size is known. Although it looks almost identical to Slovin’s formula, it has a stronger statistical foundation because it was derived from Cochran’s formula under the assumptions of a 95% confidence level and maximum variability (p = 0.5).
The Taro Yamane formula is given by:
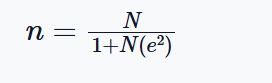
Note. This formula is especially useful for finite populations, such as schools, organizations, or specific geographic groups. It’s popular in academic research, government surveys, and social science studies because it is simple, accurate, and easy to apply.
Taro Yamane Formula Example
Scenario: Assume you are surveying all households in a small town with N = 2,000 households. You want a 5% margin of error (e = 0.05). The required sample size using the Taro Yamane’s formula can be calculated as follows:
By definition, the Taro Yamane’s formula is:
$n = \frac{N}{1 + N(e)^2}$
Substituting the values, we have:
$n = \frac{2000}{1 + 2000(0.05)^2}$
Next, compute the value of n as follows:
$n = \frac{2000}{1 + 2000(0.0025)}$
$n= \frac{2000}{1 + 5}$
$ = \frac{2000}{6}$
Thus, n = 333.333
Now, rounding up to the nearest whole number, the required sample size is 334 households.
Want to skip manual computation? Use our Taro Yamane Sample Size Calculator to instantly find your sample size and view a step-by-step solution for your chosen population and margin of error.
Comparison of Cochran’s, Slovin’s, and Taro Yamane Formulas
Choosing the right sample size formula can be confusing, especially since Cochran’s, Slovin’s, and Taro Yamane’s formulas often look similar at first glance. However, each one serves a unique purpose depending on your population size, available data, and desired level of precision. Understanding when to use each formula helps ensure your research results are accurate, valid, and statistically sound.
Below is a simple comparison table showing how these formulas differ and when to use them:
| Feature | Cochran’s Formula | Slovin’s Formula | Taro Yamane Formula |
|---|---|---|---|
| Best for | Large or infinite populations | Surveys with unknown variance | Finite populations |
| Requires Z-score? | Yes | No | No |
| Assumes normal distribution? | Yes | Not strictly | Not strictly |
| Formula type | Statistical (proportion-based) | Heuristic estimate | Simplified (95% confidence) |
| Use Case Example | National or large-scale surveys | Small business or classroom studies | Academic research with known population size (N) |
How to Determine Sample Size for Your Study
Determining the right sample size doesn’t have to be complicated. Once you understand the basic steps, you can confidently calculate how many people or items to include in your study. Whether you’re conducting a survey, an experiment, or academic research, following a simple process helps you get accurate and reliable results.
Here’s a clear, step-by-step guide to help you determine your sample size:
- Define your population size (N). Start by identifying the total number of people, items, or observations in your target group. For example, if you’re studying students in a school of 2,000, your population size (N) is 2,000.
- Decide your confidence level and margin of error. Most studies use a 95% confidence level and a 5% margin of error, but you can adjust these depending on how precise you want your results to be. A higher confidence level or smaller margin of error requires a larger sample.
- Choose the right formula. Select the formula that matches your situation. Specifically,
- Use Cochran’s formula for large or unknown populations.
- Use Slovin’s formula when you know the population size but have limited information about its variability.
- Use Taro Yamane’s formula for finite populations with a known size.
- Plug in the values and calculate. Substitute your chosen parameters into the formula or simply use our free online sample size calculators for instant results and step-by-step solutions.
- Adjust for non-response (if applicable). If you expect that not everyone will respond to your survey or participate in your study, increase your sample size slightly to compensate. For instance, if you expect a 10% non-response rate, divide your calculated sample size by 0.9 to get your adjusted value.
💡 Tip: Using a sample size calculator ensures you apply the right formula and reduces human error. This consequently saves you time and improve accuracy.
Frequently Asked Questions (FAQs)
Sample size determination is the process of calculating how many participants, items, or observations are needed in a study. It helps researchers ensure that their findings are reliable, valid, and generalizable. A well-determined sample size increases the accuracy of conclusions while minimizing time and resources.
The three most common formulas are:
– Cochran’s Formula for large or infinite populations.
– Slovin’s Formula for quick estimation when population variability is unknown.
– Taro Yamane’s Formula for finite populations with known size.
You can use any of these depending on your study design and population size.
Key factors include:
– Population size (N) – the total number of units in your target group.
– Confidence level – how sure you want to be about your results (e.g., 95%).
– Margin of error (e) – how much error you can tolerate.
– Population variability (p) – how diverse your population responses are.
– Expected non-response rate – the percentage of participants who might not respond
Cochran’s formula is the most statistically rigorous and uses a Z-score for confidence levels. Slovin’s and Taro Yamane formulas are simplified versions that don’t require a Z-score. Taro Yamane’s is specifically derived from Cochran’s formula assuming a 95% confidence level and p = 0.5.
To adjust for expected non-response, divide your calculated sample size by the anticipated response rate.
For example, if you expect 80% of people to respond and your sample size is 400:
$n_{adjusted} = \frac{400}{0.8} = 500$
Thus, you should target 500 people to get 400 responses.
