The binomial distribution is one of the most important ideas in probability and statistics. It describes situations where there are only two possible outcomes, such as success or failure, win or lose, or yes or no. This makes it very useful for studying real-life problems like coin flips, medical trials, or customer choices. Understanding the binomial distribution helps students and researchers calculate probabilities, predict outcomes, and make better decisions based on data. In this article, we explain what the binomial distribution is, its main conditions, the formula, and examples demonstrating its application. The article also shows how to derive the mean and variance of the binomial distribution.
Definition: Binomial Distribution
The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials. Each trial has only two possible outcomes, often called success and failure, and the probability of success remains the same in every trial. It is commonly written as X∼B(n, p), where n is the number of trials and p is the probability of success. This distribution is widely used in situations like coin tossing, medical testing, and quality control.
Conditions for a Binomial Distribution
Not every situation can be modeled with a binomial distribution. For it to apply, a few important conditions must be met. These rules make sure the probabilities are consistent and the results are reliable. The 4 main conditions for a binomial probability distribution are:
- Fixed number of trials – the experiment is repeated a set number of times.
- Two possible outcomes – each trial results in either success or failure.
- Constant probability of success – the chance of success stays the same in every trial.
- Independence of trials – the outcome of one trial does not affect the others.
Binomial Distribution Formula
The binomial distribution formula, also known as the binomial probability formula, is used to calculate the probability of getting a certain number of successes in a fixed number of trials. It is the foundation of the binomial distribution and is widely applied in statistics, probability theory, and real-life problem solving.
The formula is:
$$ P(X = k) = \binom{n}{k} \, p^k (1-p)^{n-k}$$
Where:
- n is the total number of trials or experiments.
- k is the number of successes we are calculating the probability for.
- p is the probability of success in a single trial.
- (1−p) is the probability of failure in a single trial.
- $$\binom{n}{k}$$ is the number of different ways k successes can occur in n trials, also called “n choose k.”
The combination
$$ \binom{n}{k}$$ is calculated using the formula: $$\binom{n}{k} = \frac{n!}{k!(n-k)!}$$
where n! (n factorial) means multiplying all positive integers from 1 up to n.
Example 1: Coin Toss
If you flip a fair coin (p=0.5) 5 times, what is the probability of getting exactly 3 heads?
Solution
In this case, n = 5, p = 0.5, and X = 3
Now, using the binomial distribution formula, we have:
$$P(X = 3) = \binom{5}{3} (0.5)^3 (0.5)^2 $$
$$= 10 \times 0.125 \times 0.25$$
$$= 0.3125$$
So, the probability is 31.25%.
Example 2: Basketball Player
A basketball player makes a free throw with probability p=0.8. If she takes 4 shots, what is the probability of making exactly 2?
Solution
Based on the question, n = 4, p = 0.8, and X = 2.
Applying the binomial probability formula, we have:
$$P(X = 2) = \binom{4}{2} (0.8)^2 (0.2)^2$$
$$ = 6 \times 0.64 \times 0.04$$
$$= 0.1536$$
So, the probability is about 15.36%.
Cumulative Probability
Sometimes, we are interested in the probability of getting at most or at least a certain number of successes. For this, we add up individual probabilities:
$$P(X \leq k) = \sum_{i=0}^{k} \binom{n}{i} p^i (1-p)^{n-i}$$
This is known as the cumulative binomial probability. For large values of n, this calculation can be time-consuming. However, with our free Binomial Distribution Calculator, you can easily compute any cumulative probability with just a few clicks.
Mean and Variance of the Binomial Distribution
The mean and variance of a binomial distribution describe its average behavior and variability. The mean, also called the expected value, tells us the typical number of successes we can expect from repeated trials. On the other hand, the variance shows how much the outcomes are likely to spread around the mean. These two measures are essential because they summarize the distribution in simple numbers and help us compare theory with observed data.
Below, we derive the mean and variance assuming the binomial conditions hold (fixed n, constant p, independent trials). We use indicator variables because the derivation is simple and clear.
Mean (Expected value)
Let X be the number of successes in n trials. We start by writing X as a sum of indicators: $$X = \sum_{i=1}^{n} X_i $$
Where Xi=1 if trial i is a success, and Xi=0 otherwise.
For one Bernoulli trial, the expectation is calculated as follows:
$$E[X_i] = 1\cdot p + 0\cdot(1-p) = p$$
Now, using the linearity of expectation, we add the expectations as follows:
$$ E[X] = \sum_{i=1}^{n} E[X_i] = n \times p.$$
Hence, the mean of binomial distribution is $$\boxed{E[X]=np}$$
Variance
By definition, $$ \operatorname{Var}(X)=E[X^2]-(E[X])^2$$
Expanding the \[X^2\], we have:
$$X^2 = \left(\sum_{i=1}^n X_i\right)^2$$
$$= \sum_{i=1}^n X_i^2 + 2\sum_{1\le i<j\le n} X_iX_j.$$
Note that for indicators $$X_i^2=X_i.$$
Thus, taking expectation, we have:
$$E[X^2] = \sum_{i=1}^n E[X_i] + 2\sum_{i<j} E[X_iX_j].$$
Since binomial trials are independent, $$E[X_iX_j]=E[X_i]E[X_j]=p^2$$ for i≠j.
Also, there are $$\binom{n}{2}=\frac{n(n-1)}{2}$$ pairs.
So, $$E[X^2] = n p + 2\cdot \binom{n}{2} p^2.$$
$$= n p + n(n-1)p^2.$$
Now, computing the variance, we have:
$$\operatorname{Var}(X)=E[X^2]-(E[X])^2$$
$$=\big(n p + n(n-1)p^2\big) – (n p)^2.$$
Simplifying the algebra, we have:
$$\operatorname{Var}(X)=n p + n(n-1)p^2 – n^2p^2 $$
$$= n p – n p^2$$
$$ = n p(1-p).$$
Thus, the variance is: $$\boxed{\operatorname{Var}(X)=np(1-p)}$$.
The standard deviation is obtained by finding the square root of the variance as shown below:
$$\sigma=\sqrt{np(1-p)}$$
Numeric example (stepwise)
If n=10 and p=0.3
- The mean of the binomial is: $$E[X]=10\times0.3=3$$
- The variance of the binomial is calculated as: $$\operatorname{Var}(X)=10\times0.3\times0.7=10\times0.21=2.1$$
- The standard deviation is: $$\sigma=\sqrt{2.1}\approx 1.449.$$
A light bulb manufacturer knows that about 3% of bulbs are defective. A quality inspector randomly tests 20 bulbs from a shipment. Let X be the number of defective bulbs found.
Answer the following questions:
i) What is the probability that at most 2 bulbs are defective?
ii) What is the probability that exactly 2 bulbs are defective?
iii) What is the probability that at least 3 bulbs are defective?
iv) What is the probability that less than 2 bulbs are defective?
v) What is the probability that greater than 1 bulbs is defective?
From the problem, we know that
- n = 20 is the number of trials
- p = 0.03 is the probability of success, i.e. defective bulb
- q = 1-p = 0.97 is the probability of failure, i.e. non-defective bulb
The random variable (X) represents the number of defective bulbs out of 20.
(i) What is the probability that at most 2 bulbs are defective?
This question requires us to compute P(X≤2)
Thus, n = 20, p = 0.03, and k = 2
To solve the problem manually, we follow this procedure:
(i) At most 2
P(X≤2) = P(X=0)+P(X=1)+P(X=2)
P(X=0) =$\binom{20}{0}(0.03)^0(0.97)^{20}$
P(X=1) = $\binom{20}{1}(0.03)^1(0.97)^{19}$
P(X=2) = $\binom{20}{2}(0.03)^2(0.97)^{18} $
Thus:
P(X≤2) = 0.543794 + 0.336368 + 0.098830
= 0.978992
Now using our binomial distribution calculator, simply enter the number of trials (n = 20), probability of success (p = 0.03), and the number of successes (k = 2). Then hit the “calculate” button:
You’ll get the following outputs:
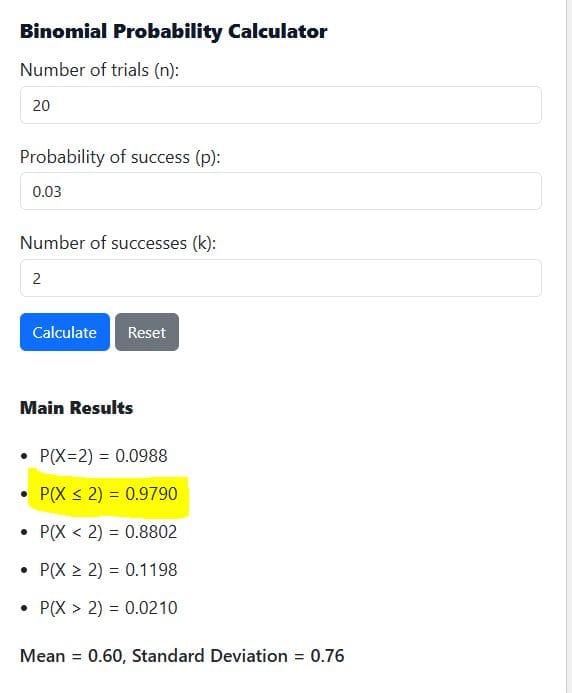
As you can see, the required probability is 0.9790, which coincide with the manual calculation.
ii) What is the probability that exactly 2 bulbs are defective?
This question requires us to compute p (X=2)
Thus, n = 20, p = 0.03, and k = 2
To solve the question manually, we have:
P(X=2) = $\binom{20}{2}(0.03)^2(0.97)^{18}$
$= 190 \times (0.03)^2 \times (0.97)^{18}$
= 0.098830
Now, using our binomial probability calculator, you simply need to insert n = 20, p = 0.03, and k =2 and look for the P(X=2) from the results, as shown below:
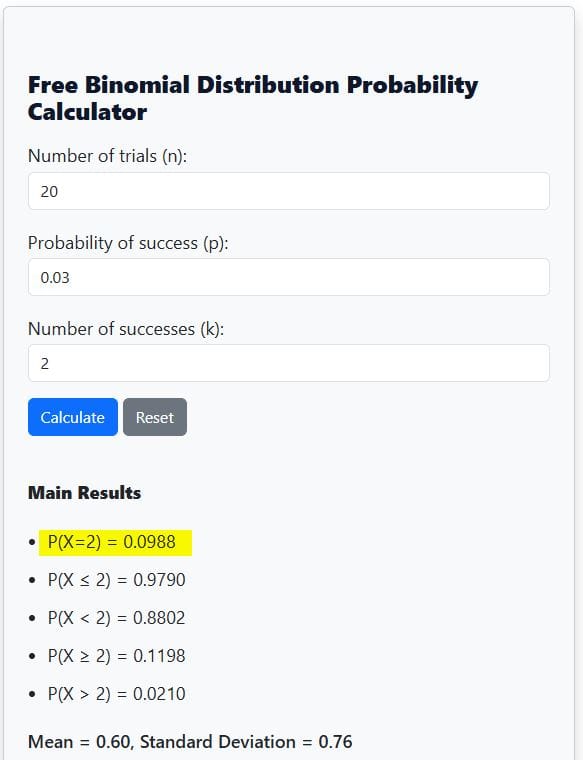
Now, you can see that both the manual computation and our free calculator yield the same values. In other words, P(X = 2) = 0.0988 in both cases.
iii) What is the probability that at least 3 bulbs are defective?
Here, we need to find P(X≥3)
Thus, n =20, p = 0.03, and k = 3
Substituting the values in the binomial distribution probability formula, we have:
P(X≥3) = 1 – P(X≤2)
= 1 – (P(X=0)+P(X=1)+P(X=2))
But from (i), we know that:
P(≤2) = 0.978992
Thus, P(X≥3) =1- 0.978992
=0.021008
Now, using our online binomial probability calculator, we simply input n = 20, p = 0.03, and k =3. Next, hit the “Calculate” button to see the results. You can then read the required probability from the results (i.e. P(X≥3)) as shown below:
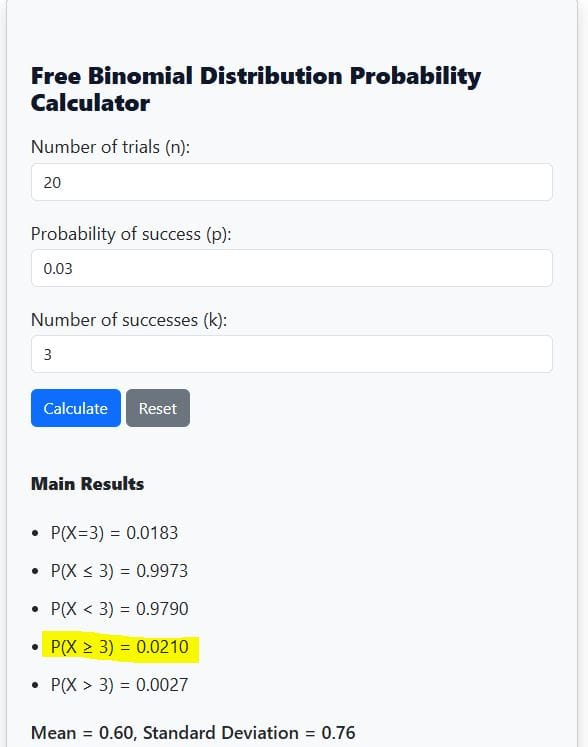
As you’ll note, the manual calculation and the calculator still yield the same results (0.0210). This implies that you can always use our binomial calculator to verify manual calculation results.
iv) What is the probability that less than 2 bulbs are defective?
This question requires you to calculate P(X < 2). This is equivalent to finding P(X≤1).
From the question, we know that: n = 20, p = 0.03, and k =2
And P(X≤1) = P(X=0) + P(X=1)
From (i), P(X=0) =0.543794 and P(X=1) = 0.336368
Thus, the required P(X<2) is given by:
P(X<2) = 0.543794 + 0.336368
=0.880162
Using our binomial distribution calculator, we only need to specify the given values. That is, n = 20, p =0.03, and k =2. Next, read the values corresponding to P(X<2), as shown below:
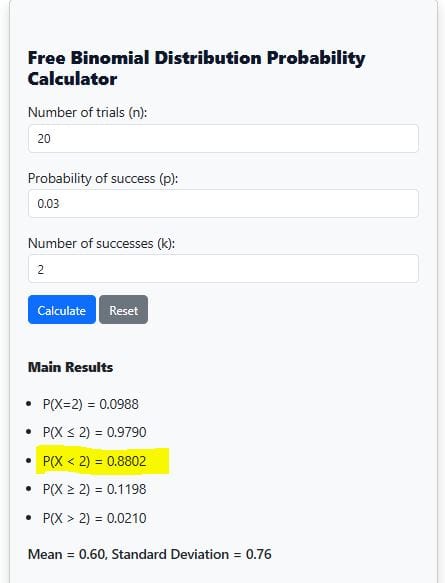
The calculator still show results that are consistent with manual calculation. In other words, both manual calculation and our binomial probability calculator reveal that P(X<2) = 0.8802.
v) What is the probability that greater than 1 bulbs is defective?
Here, we need to find P(X>1). But we know that n = 20, k =1, and p = 0.03
P(X>1) can be redefined as follows:
P(x>1) = 1−P(X≤1))
Where, P(X≤1) = P(X=0) + P(X=1)
But from (iv), P(X≤1) = 0.880162
Thus:
P(X>1) = 1 – 0.880162
= 0.119838
Using Our Free Binomial Distribution Probability Calculator, simply specify, n = 20, p = 0.03, and k = 1. Once you hit the “Calculate” button, you’ll only need to read P(X>1), as shown below:
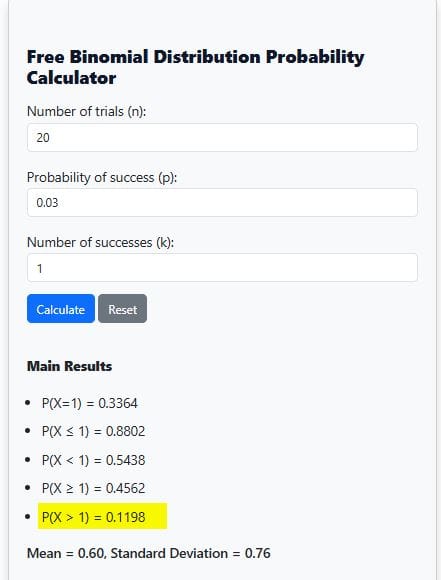
Just as the manual computation using the binomial formula, our free binomial calculator yielded the same findings. That is, P(X>1) = 0.1198.
Applications of Binomial Distribution
The binomial distribution has wide applications across different fields because many real-life situations can be reduced to success and failure outcomes. By providing a framework for modeling probabilities over repeated independent trials, it enables researchers, professionals, and decision-makers to make informed predictions and draw meaningful conclusions. Below are some key areas where the binomial distribution is applied:
- Business – Customer Purchase Probability
Businesses often use the binomial distribution to predict how many customers will make a purchase. For example, if a company knows that 20% of visitors to their online store typically buy a product, they can model the probability that exactly 50 out of 200 visitors will purchase. This helps in sales forecasting, inventory planning, and marketing strategies. - Medicine – Success/Failure in Clinical Trials
In medical research, clinical trials test whether a treatment is effective. The binomial distribution can model the probability of a certain number of patients responding positively to a new drug. This helps researchers estimate effectiveness and assess risks before a treatment is approved. - Education – Exam Performance
Teachers or educational researchers might use the binomial distribution to calculate the probability of a certain number of students passing an exam. For example, if the probability of a student passing is 0.7, the distribution can help predict how many students out of a class of 30 are likely to succeed. - Quality Control – Defective Products
Manufacturers use the binomial distribution to estimate the number of defective items in a production batch. If the probability of a defect is known, they can determine the likelihood of finding a certain number of defective products, which is vital for maintaining quality standards.
Conclusion
The binomial distribution is one of the most important concepts in probability and statistics. It provides a simple yet powerful way to model situations where there are only two possible outcomes, such as success or failure, win or lose, pass or fail. By understanding its definition, conditions, formula, mean, variance, and real-world applications, you can see how this distribution applies to both academic study and practical decision-making.
Frequently Asked Questions
A binomial distribution is a probability model that describes the number of successes in a fixed number of independent trials, where each trial has only two possible outcomes: success or failure.
The key conditions are:
– a fixed number of trials
– each trial has two outcomes
– the probability of success is constant
– all trials are independent.
The probability mass function is:
$$ P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}$$
Where:
– n is the number of trials
– k is the number of successes
– p is the probability of success.
The mean of a binomial distribution is n×p, and the variance is n×p×(1−p). These values summarize the expected outcome and variability of the distribution.
It is used in many fields such as business (predicting customer purchases), medicine (clinical trials), education (exam pass rates), and manufacturing (quality control).
The binomial distribution is discrete mainly used when outcomes are limited to success or failure. On the other hand, the normal distribution is continuous probability distribution that models data that follow a bell-shaped curve. Under certain conditions, the binomial distribution can be approximated by the normal distribution.
