Z Critical Value Calculator

Use our Z Critical Value Calculator to quickly find one-tailed and two-tailed Z critical values for any significance level (α). This tool saves you time by instantly computing the critical value without relying on Z tables. It is perfect for students, researchers, and anyone performing hypothesis testing or calculating confidence intervals.

What is Z Critical Value?

A Z critical value is the point on the standard normal curve that marks the boundary between the rejection and acceptance regions in a hypothesis test. It shows the threshold beyond which results are statistically significant. It is also used to calculate the margin of error when determining confidence intervals for a population mean or proportion.

How to Use the Z Critical Value Calculator

Using our calculator is quick and simple. Follow these steps to get your Z critical value:

1. Enter the significance level (α): This is usually 0.05 for a 95% confidence level.
2. Select the type of test: Choose one-tailed or two-tailed depending on your hypothesis.
3. Click “Calculate”: The calculator will instantly show the Z critical value.
4. View step-by-step explanation: The calculator also shows how the value was determined.

For example: If you enter α = 0.05 and select a two-tailed test, the calculator will show Z = ±1.96. This value indicates the cutoff points beyond which your test statistic would be considered statistically significant.

Quick Example: Finding Z Critical Value Using the Calculator

This section shows how to apply the Z Critical Value Calculator in both hypothesis testing and confidence interval calculation. Each example demonstrates how the calculator helps you make decisions and interpret results.

Two-Tailed Hypothesis Test Example

A school implements a new teaching method and wants to see if it changes student exam scores. The teacher calculates Z test statistic = 1.90. At a 5% significance level, can we conclude that the new method changes exam scores? (Use the critical value approach.)

Solution

1. State the Hypotheses
   • Null hypothesis (H₀): μ = current exam mean
   • Alternative hypothesis (H₁): μ ≠ current exam mean
2. Identify the Type of Test: This is a two-tailed test with α = 0.05
3. Identify the Z test statistic: From the scenario, the z statistic = 1.90
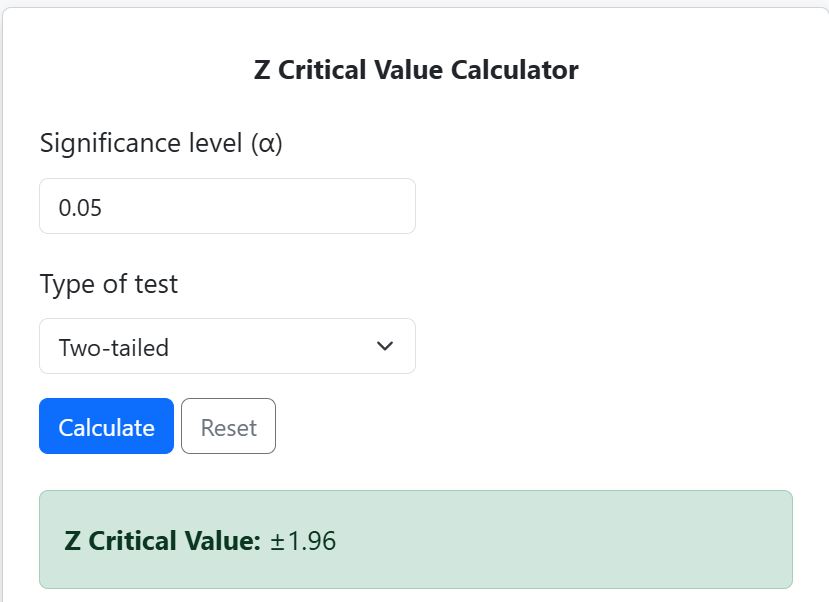
4. Find Z Critical Value: Using the calculator, the Z-critical values are ±1.96 (see Figure 1)
5. Decision Rule: If Z test statistic < -1.96 or > 1.96, we should reject H₀. Otherwisem we fail to reject H₀
6. Compare Z Statistic with Critical Value: Since the z test statistic (1.90) is within ±1.96, we fail to reject H₀
7. Conclusion: There is not enough evidence to say the new teaching method changes exam scores.

Right-Tailed Hypothesis Test Example

A tutoring program wants to see if it increases student math scores. The computed Z test statistic = 3.0. At 5% significance level, can we conclude the program improves scores?

Solution

1. State the Hypotheses
   • H₀: μ ≤ current mean score
   • H₁: μ > current mean score
2. Identify the Significance Level (α) and Type of Test: This is a right-tailed test (one-sided) with α = 0.05
3. Identify the z test statistic: z test statistic = 3.0
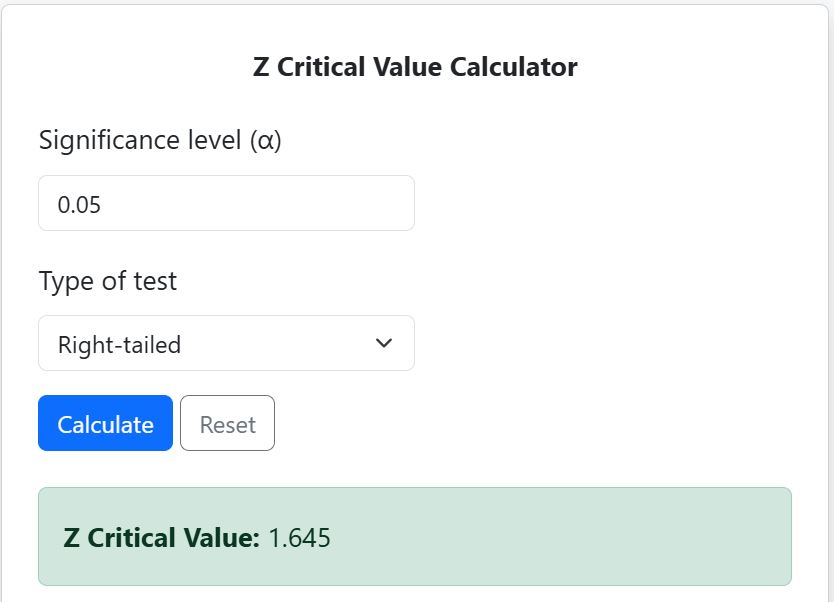
4. Find Z Critical Value: Using the calculator, the z-critical value is 1.645 (See Figure 2)
5. Decision Rule: If Z > 1.645, we reject H₀. Otherwise, we fail to reject H₀
6. Compare Z Statistic with Critical Value: Since the z test statistic (Z = 3.0) is greater than z-critical value (1.645), we reject H₀
7. Conclusion. The tutoring program significantly increases scores at 5% significance.

Left-Tailed Hypothesis Test Example

A nutritionist tests whether a new diet reduces cholesterol. The computed Z test statistic = -3.125. At 5% significance level, can we conclude the diet lowers cholesterol?

Solution

1. State the Hypotheses
   • H₀: μ ≥ population mean cholesterol
   • H₁: μ < population mean cholesterol
2. Identify the type of test and Significance Level (α): This is a one-sided (left-tailed) test. α = 0.05
3. Identify the Z test statistic: From the scenario, the z test statistic is -3.125
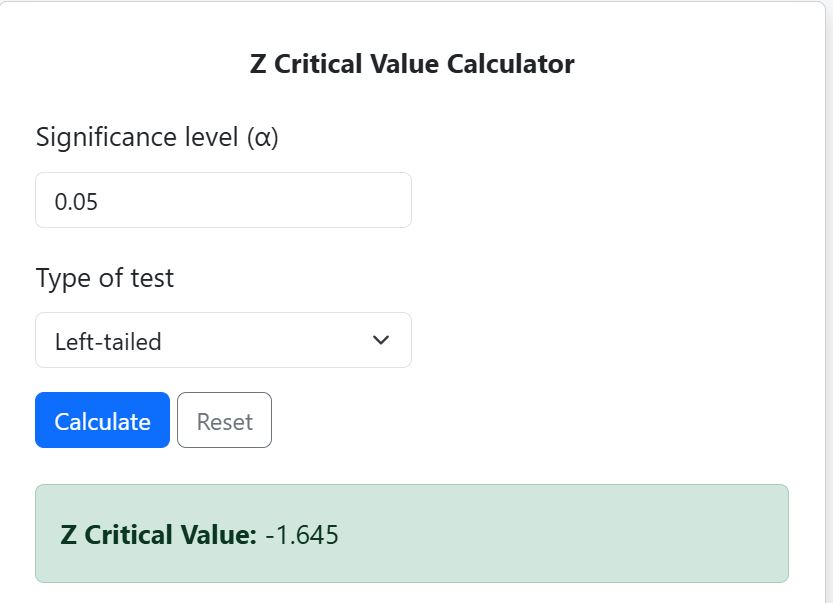
4. Find Z Critical Value: Using the calculator, the z critical value is -1.645 (see Figure 3).
5. Decision Rule: If Z < -1.645, we reject H₀. Else, we fail to reject H₀
6. Compare Z Statistic with Critical Value: Since the z-test statistic (-3.125) is less than the critical value (-1.645), we Reject H₀
7. Conclusion: The diet significantly lowers cholesterol at the 5% level.

Confidence Interval Example

A researcher wants to estimate the average height of students at a university. A sample of 50 students has mean = 170 cm and population standard deviation = 6 cm. Construct a 95% confidence interval using Z critical values.

Solution

1. Identify Confidence Level: 95% → α = 0.05
2. Type of Test: Two-tailed (for confidence interval)
3. Find Z Critical Value: Use the calculator to find two-tailed critial value when α = 0.05. This gives Z critical value = ±1.96 (See Figure 1).
4. Compute Margin of Error (ME): $ME = Z_{\text{crit}} \times \frac{\sigma}{\sqrt{n}}$
   • $ = 1.96 \times \frac{6}{\sqrt{50}}$
   • $ \approx 1.66$
5. Construct Confidence Interval: $CI = \bar{X} \pm ME$
   • $ = 170 \pm 1.66$
   • = [168.34, 171.66]
6. Interpretation: We are 95% confident that the true mean height lies between 168.34 cm and 171.66 cm.

Want to Learn How to Compute Z Critical Values Manually? Check out our detailed guide on how to Compute Z Critical Values by Hand. The article shows you exactly how to find one-tailed and two-tailed Z critical values without a calculator but using z-tables.

Z Critical Values for Common Significance Levels

While the calculator can give you exact results for any alpha level, it is also helpful to have a quick reference. The table below shows the most widely used one-tailed and two-tailed z critical values at common significance levels.

Significance Level (α)	Confidence Level	One-Tailed Z Critical Value	Two-Tailed Z Critical Value
0.10	90%	1.282	±1.645
0.05	95%	1.645	±1.960
0.025	97.5%	1.960	±2.241
0.01	99%	2.326	±2.576
0.005	99.5%	2.576	±2.807
0.001	99.9%	3.090	±3.291

Tips for Using Our Z-Critical Value calculator

• Always select the correct test type: one-tailed (right or left) or two-tailed.
• Enter a valid significance level (α) between 0 and 1.
• Use the calculator to quickly verify Z critical values when solving homework, assignments, or research problems.
• For full understanding, practice computing Z critical values manually using standard normal tables alongside the calculator.

Want to learn how to calculate Z critical values in Excel step by step using NORM.S.INV(), with examples for left-tail, right-tail, and two-tailed tests? Check out our full guide here.

Frequently Asked Questions