Use this free Yamane Formula Calculator to quickly find the right sample size for your research. The calculator is based on Taro Yamane’s 1967 formula, which makes it simple to calculate the number of participants you need. Just enter your total population and your preferred margin of error. The tool will give you the sample size instantly.The calculator also provides a step-by-step explanation to help you understand how to compute the sample size, manually.
Use this calculator to find the required sample size using the Taro Yamane formula
Taro Yamane Sample Size Formula
The Taro Yamane formula is sample size estimation method for calculating the required sample size from a given population. It was developed by Taro Yamane in 1967 to provide a simple and practical approach to calculate the optimal sample size from a finite population. This formula is especially useful in survey research, academic studies, and social science investigations, where determining an appropriate number of respondents is critical to obtain reliable results. The main advantage of the Taro Yamane sample size formula is that it requires only two inputs: the total population size (N) and the desired margin of error (e).
The Yamane Formula is:
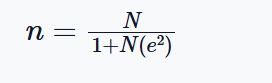
Where:
- n is the required sample size
- N is the total population size
- e is the margin of error
Alternative Sample Size Formulas
The Yamane formula is just one way to calculate the sample size for your research. It is simple and works well for most surveys. However, there are also other sample size estimation formulas that you can use to calculate the minimum sample size for your study.
For example, Slovin’s formula uses the same calculation as Yamane’s formula. In fact, the main difference between these formulas is historical and contextual. In particular, while the Yamane’s formula is often cited in academic research papers, the Slovin’s formula is widely used in practical surveys and small-scale research projects. You can try our Slovin Sample Size Calculator to see how it compares with Yamane’s formula.
Another option is the Cochran’s formula, which is especially useful for large or very diverse populations. Cochran’s method considers confidence levels and population variability, giving you a more precise sample size. Our Cochran Sample Size Calculator makes it easy to calculate step by step.
How to Calculate Sample Size Using the Yamane Formula (Step-by-Step)
Calculating the sample size using the Yamane formula is simple and straightforward. Let’s go through a step-by-step example to make it clear.
Scenario: Suppose you are conducting a survey with a total population of 10,000 people, and you want a margin of error of 5% (0.05). You can use the Yamane formula to find the required number of participants.
Solution
By definition, the Yamane’s sample size formula is:
$n = \frac{N}{1 + N(e^2)}$
From the scenario, we know that:
- The finite population size is 10,000
- The margin of error is 0.05
Substituting the known values in the formula, we have:
$n = \frac{10,000}{1 + 10,000(0.05^2)}$
$=\frac{10,000}{1 + 10,000(0.0025)}$
$=\frac{10,000}{1 + 25}$
$=\frac{10,000}{26}$
≈384.62
Rounding up to the nearest whole number, the required sample size is 385 participants.
Alternatively, using the free yamane sample size calculator, you simply need to enter the population size and the margin of error. On hitting the Calculate button, you’ll get an accurate answer with step-by-step explanation as shown below:
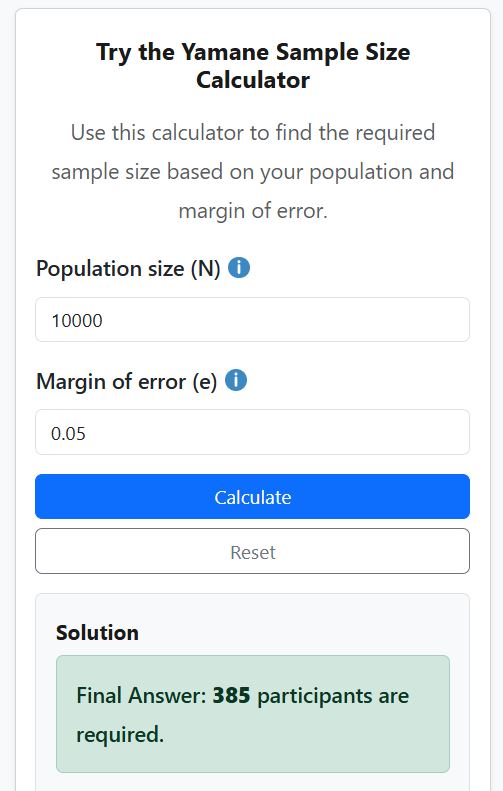
The calculator will also give you a step-by-step explanation to help you understand how to calculate the sample size by hand as shown below:

Advantages and Limitations of the Yamane Formula
The Yamane formula is a simple and effective way to calculate sample size, but like any method, it has both strengths and limitations.
Advantages:
- It is easy to apply, even for beginners.
- It requires only two inputs: the total population (N) and the margin of error (e).
- It is ideal for academic research and surveys. This helps researchers quickly determine a representative sample.
Limitations:
- The formula assumes simple random sampling. Thus, it may not be accurate for more complex sampling methods.
- It doesn’t account for design effects or population variability. This means that it may underestimate or overestimate the needed sample in some cases.
Overall, the Yamane formula is a great starting point for sample size calculation, especially when simplicity and speed are important.
Frequently Asked Questions
The Taro Yamane sample size formula is a method developed by Taro Yamane in 1967 to help researchers calculate the number of participants needed from a finite population. It is widely used in surveys, academic research, and social science studies. To calculate the sample size using this formula, you need the total population (N) and the margin of error (e). The yamane formula is:
– n = N/(1+N*e^2)
Where:
– n is the required sample size
– N is the total population
– e is the margin of error
You can use the Yamane formula when you need to quickly determine a sample size for a large, known population with a specified margin of error. It is a simple and widely used method, particularly in social sciences and surveys, but it assumes simple random sampling.
Mathematically, Yamane and Slovin’s formulas are the same. The difference is mainly in context and usage. Yamane is often used in academic research, while Slovin is commonly used in practical surveys.
Yes, it can be used for large populations, but it assumes simple random sampling. For very large or complex populations, methods like Cochran’s formula may provide more precise results.
A smaller margin of error requires a larger sample size, while a larger margin of error allows for a smaller sample. The margin of error determines the precision of your results.