This calculator finds the chi-square critical value for a given significance level and degrees of freedom. It also provides a step-by-step explanation of how to find and interpret the critical value for chi-square tests.
Enter the Significance level and degrees of freedom to calculate the chi-square critical value.
If you’re comparing results across multiple statistical tests, our combined Critical Value Calculator allows you to compute Z, T, F, Chi-square, and R critical values from a single interface.
How to Use the Chi-Square Critical Value Calculator
To find the critical value for any chi-square test using this tool, follow these steps:
- Step 1: Enter the significance level (α)
- Step 2: Enter the degrees of freedom (df)
- Step 3: Click the “Calculate” button
The calculator instantly gives you the correct critical value, along with a clear explanation of how to make a decision using the critical value.
What is a Chi-Square Critical Value?
A chi-square critical value is a threshold from the chi-square distribution used in hypothesis testing to determine whether the results are statistically significant or not. Specifically, the critical value is compared with the calculated test statistic to determine whether to reject or fail to reject the null hypothesis in a chi-squared test.
The decision is:
- Reject the null hypothesis if the calculated chi-square statistic value is greater than the chi-square critical value.
- Fail to reject the null hypothesis (H0) if the calculated chi-square statistic value is less than the chi-square critical value.
Finding Chi-Square Critical Values: Examples
Want to learn how to apply the calculator to solve exam questions on chi-square critical values? Just follow these two examples to grasp the concept.
Example 1: Goodness-of-Fit Test
Find the chi-square critical value for a goodness-of-fit test to determine if a six-sided die is fair. The die is rolled 60 times, and the significance level is 0.05.
Solution
Step 1: Identify your parameters
- Significance level (α) = 0.05
- Degrees of freedom (df). For a chi-square goodness of fit test, df = k-1, where k is the number of categories. Therefore, df = 6 − 1 = 5
Step 2: Use the calculator to find the critical value
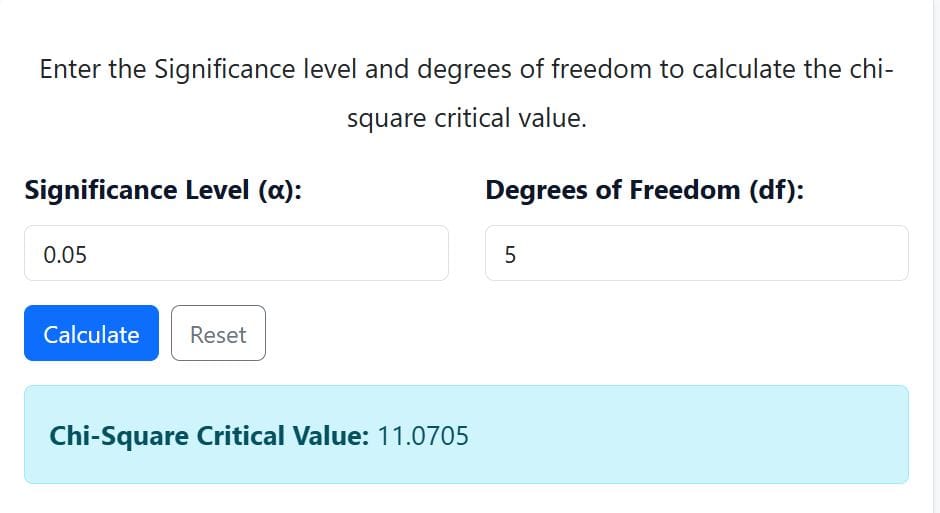
- Enter α = 0.05
- Enter df = 5
- Click “Calculate”
The calculator gives you 11.0705. Thus, χ²0.05, 5 = 11.0705
Step 3: Interpret the result
- If your calculated chi-square test statistic from your die rolls is greater than 11.0705, reject the null hypothesis and conclude that the die is not fair.
- However, if it’s less than 11.0705, there’s no evidence to conclude the die is unfair.
Example 2: Test of Independence
Find the chi-square critical value for a test of independence to determine if the study method is related to the exam outcome. A survey of 100 students’ records study method (Group vs. Solo) and exam results (Pass vs. Fail). Use a significance level of 0.01.
Solution
Step 1: Identify your parameters
- Significance level (α) = 0.01
- Degrees of freedom (df). For a chi-square test of independence, df = (r − 1) × (c − 1), where r and c are the number of categories in the rows and columns, respectively. From the question, there are two categories in each group. Hence, df = (2 − 1) × (2 − 1) = 1
Step 2: Find the Critical Value using the Calculator
To find the critical value using the calculator, follow these steps
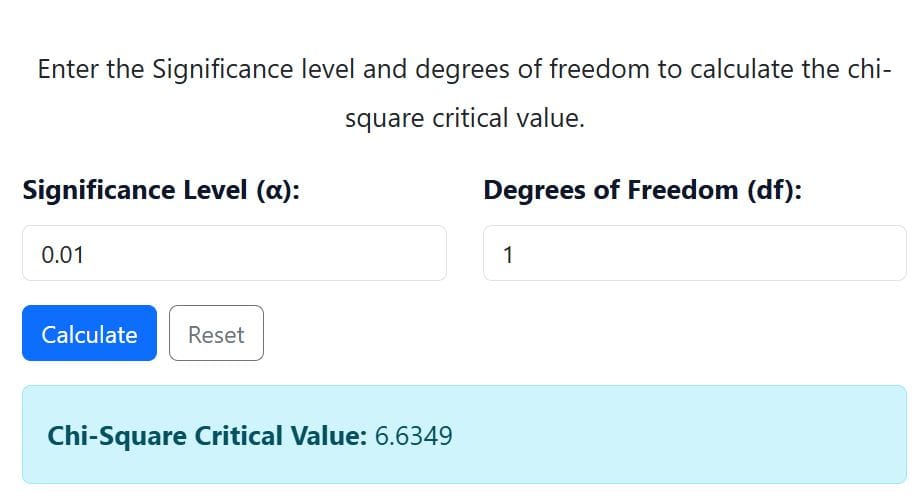
- Enter α = 0.01
- Enter df = 1
- Click “Calculate”
The critical value using the calculator is 6.6349. That is χ²0.01,1 = 6.6349
Step 3: Interpret the result
Compare the chi-square critical value with the observed chi-square test statistic.
- If your observed chi-square statistic is greater than 6.6349, reject the null hypothesis and conclude that the study method and exam results are likely related.
- However, if the observed chi-square statistic is less than 6.6349, there is no sufficient evidence to conclude that the two groups are related.
Note. You can also use a chi-square critical value table to find the critical values.
Frequently Asked Questions
Chi-square tests measure how much the observed data deviate from the expected values. Larger deviations provide stronger evidence against the null hypothesis. Because these extreme values occur on the right side of the chi-square distribution, chi-square tests are always right-tailed.
The degrees of freedom depend on the type of chi-square test. For a chi-square goodness of fit test, df = k-1, where k is the number of categories. However, for a chi-square test of independence or homogeneity, df = (number of rows − 1) × (number of columns − 1). Always make sure to use the correct df to get the correct critical value for your test.
Yes. This calculator finds critical values for the chi-square goodness-of-fit, test of independence, and test of homogeneity. You only need to make sure you enter the correct degrees of freedom and significance level to get the correct chi-square critical value.