This calculator computes the population standard deviation (σ) for your data. Enter the data and click the “Calculate” button to get instant results, with a clear step-by-step solution.
Enter your data values separated by commas, spaces, or tabs (you can copy-paste from Excel).
Want to calculate the sample standard deviation instead? Use the sample standard deviation calculator for instant results and a step-by-step solution.
How to Use the Population Standard Deviation Calculator
To find the population standard deviation using the calculator, follow these simple steps:
- Step 1. Enter the data (You can separate it by commas, spaces, tabs, or even copy-paste from Excel).
- Step 2. Click the “Calculate” button
This tool will give you instant results, along with a clear step-by-step explanation of how to calculate the population standard deviation by hand.
What is Population Standard Deviation?
Population standard deviation is one of the statistical measures of dispersion, which quantifies the amount of variation in an entire dataset (population) relative to its population mean. In other words, it indicates how tightly data points are clustered around the population average, with higher values representing greater variability.
Population vs. Sample Standard Deviation
While both population and sample standard deviation measure how spread out the data is, they differ in what they represent and their formulas. Here are the key differences:
- Population Standard Deviation (σ) is used when you have the entire dataset from the population. The formula divides the sum of squared deviations by N (total number of observations in the population)
- The sample standard deviation is used when you have sample data drawn from the population. The formula divides the sum of squared deviations by n-1 (n is the sample size) instead of N. This helps to account for the fact that a sample is only an estimate of the population.
Population Standard Deviation Formula
The formula for the population standard deviation (σ) is:
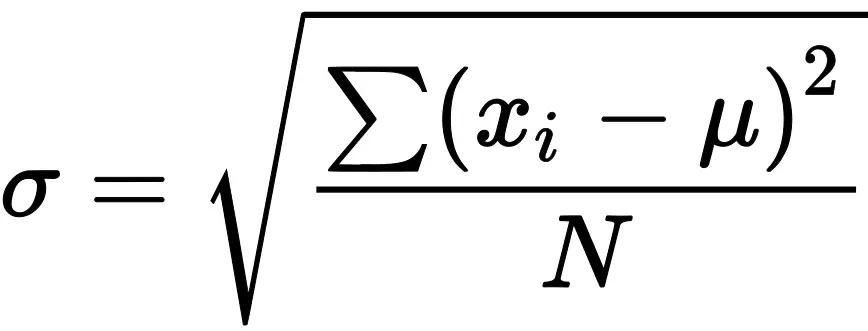
Where:
- σ is the population standard deviation
- N is the total number of observations in the population
- xi is each individual value in the population
- μ is the population mean (average of all values)
How to Calculate Population Standard Deviation
While you can quickly find the population standard deviation using the above calculator, it is good to learn how to compute it manually. The following example shows you how to compute the population standard deviation by hand, step-by-step.
Example. Calculate the standard deviation for the following population data.
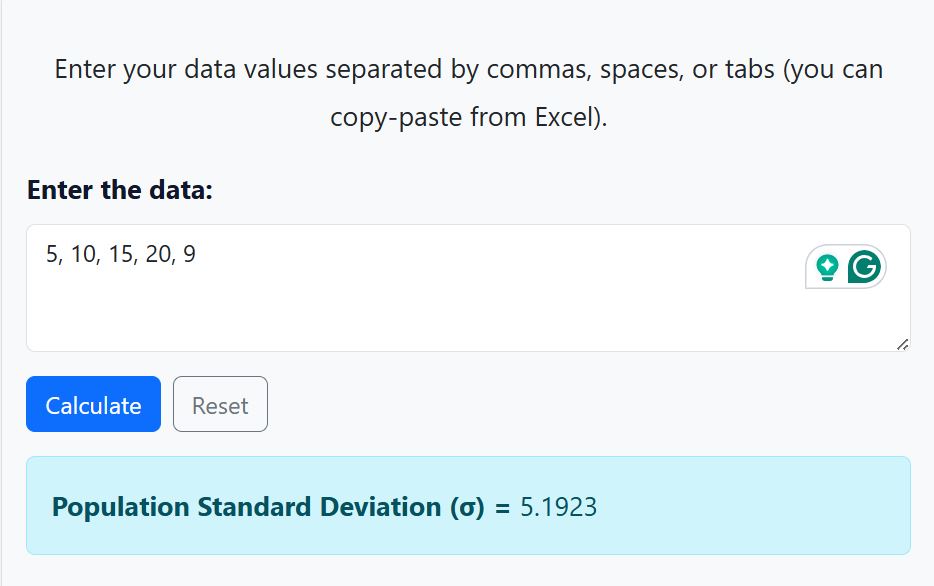
Dataset. 5, 10, 15, 20, 9
Solution
Step 1. Calculate the Population Mean
The population mean formula is μ=∑xi/N
Where:
- N is the total number of observations
- ∑xi is the sum of all observations
From our dataset:
∑xi = 5 + 10 + 15 + 20 + 9
= 59
Also, N = 5 since there are only 5 observations in the data
Thus, the population mean, μ = 59/5
=11.8
Step 2. Calculate the Sum of Squared Deviations
From the population standard deviation formula, the sum of squared deviation formula is: ∑(xi−μ)2
This means we need to subtract the population mean (11.8) from each value, square the results, and sum all the squared deviations.
The table below shows how to compute deviations from the population mean and the squared deviations.
Note. We substituted μ with 11.8
| xi | xi−11.8 | (xi−11.8)2 |
|---|---|---|
| 5 | 5-11.8 = -6.8 | (-6.8)2 = 46.24 |
| 10 | 10-11.8 = -1.8 | (-1.8)2 = 3.24 |
| 15 | 15-11.8 = 3.2 | (3.2)2 = 10.24 |
| 20 | 20-11.8 = 8.2 | (8.2)2 = 67.24 |
| 9 | 9-11.8 = -2.8 | (-2.8)2 = 7.84 |
To find the sum of the squared deviations, we need to sum the values in the column, (xi−11.8)2
Thus, ∑(xi−μ)2 = 46.24 + 3.24 + 10.24 + 67.24 +7.84
= 134.8
Step 3. Divide the sum of squared deviations by N
Dividing the sum of squared deviations by N gives you the population variance, σ2
Therefore, σ2 = ∑(xi−μ)2/N
= 134.8/5
= 26.96
Step 4. Find the Population Standard Deviation
The population standard deviation is the square root of the population variance.
Since the results in step 3 are the population variance, we can find the population standard deviation by finding the square root of 26.96.
Thus, σ=√(26.96)
= 5.1923
Therefore, the population standard deviation of the data is approximately 5.1923.
Alternatively, if you only need quick solutions, just copy-paste the values in the calculator and click the “calculate” button. The calculator will yield similar results, as shown below.
Frequently Asked Questions
Population standard deviation measures how much the values in an entire population vary from the population mean. It helps understand the overall variability or spread of data.
Population standard deviation uses N (the total number of values) in the denominator, while sample standard deviation uses n−1.
To calculate population standard deviation, follow these steps:
Step 1. Find the population mean.
Step 2. Subtract the mean from each value and square the result.
Step 3. Sum all squared deviations.
Step 4. Divide the sum by the total number of values (N).
Step 5. Take the square root of the result.
No. This calculator is specifically for population standard deviation. If you have a sample, you should use a sample standard deviation calculator, which divides by n−1 instead of N.