This calculator converts any fraction (proper/improper) into decimal equivalents. Just enter any fraction and click “convert” to get instant results with step-by-step explanation.
The step-by-step explanation will help you learn how to turn any fraction into a decimal by hand.
Enter a fraction you want to convert to a decimal and click "Convert"
Want to convert a decimal back to its fraction equivalent? Use the decimal to fraction calculator.
How to Use the Fraction to Decimal Calculator
To turn any fraction to a decimal using the calculator, follow these steps:
- Step 1: Enter the fraction either as a proper or an improper fraction
- Step 2: Click the “Convert” button.
The calculator will instantly give you the decimal equivalent of the fraction, along with a step-by-step explanation of how convert your fraction to a decimal manually, without using the calculator.
How to Convert a Fraction to a Decimal
Want to learn how to convert a fraction to a decimal manually, without using the calculator? Follow these steps:
- Identify the numerator (top number) and the denominator (bottom number)
- Divide the numerator by the denominator using the long division method until you reach a remainder of 0.
Special Cases
While the above steps apply to any fraction, there are various cases when conversion might be faster. Here are the special cases you should consider when turning a fraction into a decimal:
- Case 1: Mixed Numbers. To convert a mixed number to a decimal, you can either convert the mixed number to an improper fraction and use the long division method, or keep the whole number separate and convert the proper fraction part into a decimal using the long division method.
- Case 2: Repeating Decimals. If the division does not end (recurs), identify the repeating digit(s) and place a bar over them. For instance, the fraction 1/3 = 0.333… in decimal form. As you can see, the digit 3 is recurring, and hence, you should write the answer as 0.3 with a bar on top of 3.
- Case 3: Reducing Fractions. In some situations, you may find that the fraction you want to convert into a decimal is not simplified. In this case, you need to simplify the fraction to its lowest terms first to make the division easier. For instance, to convert 3/9 into a decimal, simplify it first to 1/3 and then apply the long division method.
Examples: Converting Fractions to Decimals
Still not confident in converting fractions to decimals? Let’s walk through a few examples to help you learn how the conversion works in different situations.
Example 1: Converting a Simple Fraction to a Decimal
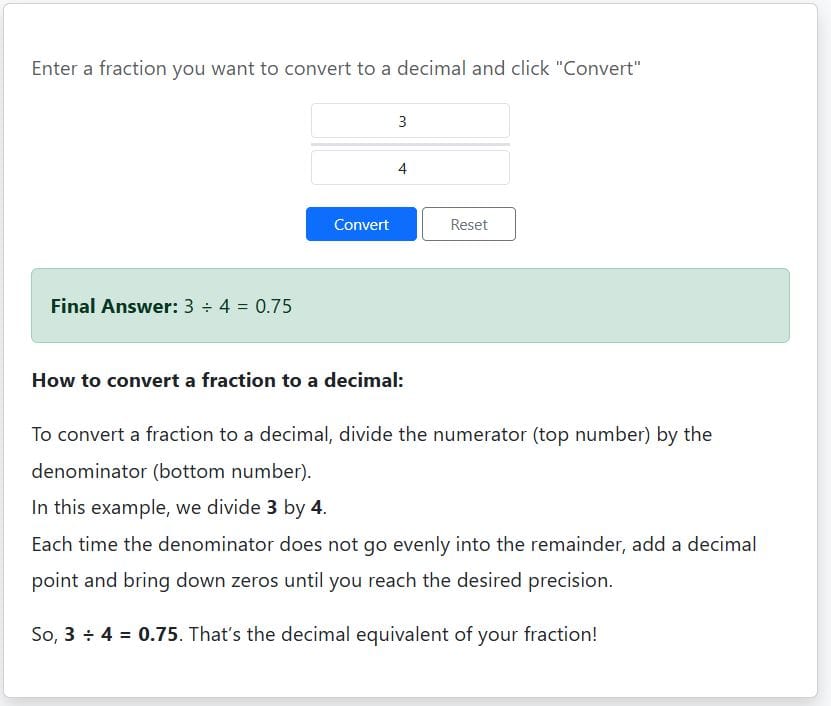
Convert 3/4 to a decimal.
Solution
Step 1: Identify the Numerator and denominator
From the question, the numerator is 3, and the denominator is 4.
Step 2: Divide the numerator by the denominator using the long division method.
That’s 3÷4 = 0.75
Since the long division stops neatly, we get a terminating decimal.
Therefore, 3/4 as a decimal is 0.75
Alternatively, you can enter the fraction 3/4 into the fraction to decimal calculator to get instant results with step-by-step explanation as shown below:
Example 2: Converting a Mixed Number to a Decimal
Convert 2(1/5) to a decimal.
Solution
To convert the mixed number, 2(1/5) to a decimal, follow these steps:
Step 1: Keep the whole number aside.
In this case, 2 is the whole number.
Step 2: Convert the proper fraction part to a decimal.
In this case, we only need to convert 1/5 into its decimal equivalent.
Using long division, 1÷5 = 0.2
Step 3: Add the whole number to the decimal
The whole number is 2, and the decimal equivalent of 1/5 is 0.2.
Adding these two numbers, we have: 2+ 0.2
= 2.2.
Therefore, the decimal equivalent of the mixed number, 2(1/5), is 2.2.
You’ll also get similar results by first converting the mixed number to an improper fraction and applying the long division. To verify this, follow these steps:
Step 1: Convert the mixed number into an improper fraction.
2(1/5) into an improper fraction becomes 11/5
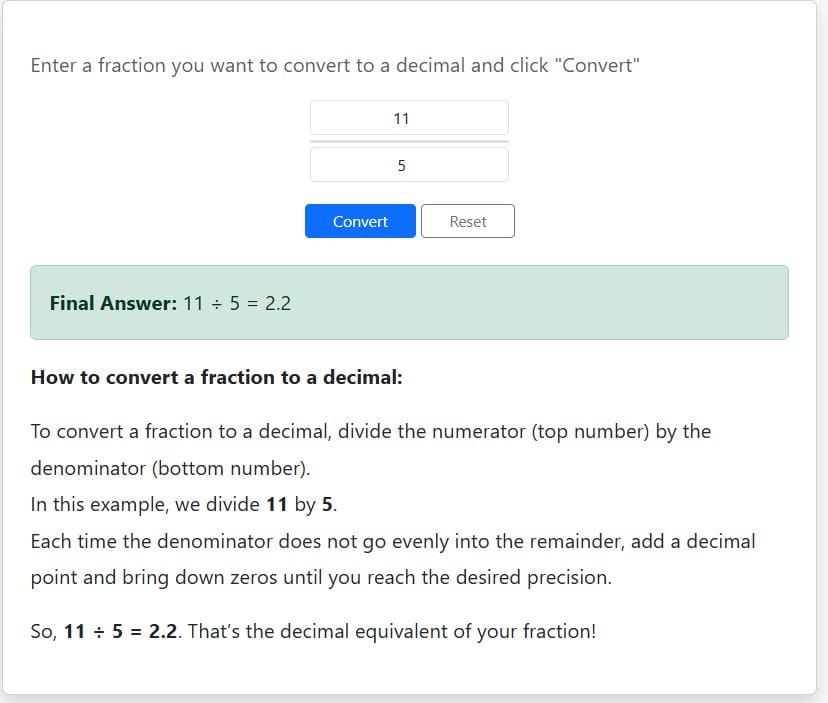
Step 2: Divide the numerator (11) by the denominator (5)
Dividing 11/5 using long division or the online fraction-decimal calculator gives 2.2 as shown below:
Example 3: Converting a Repeating Fraction to a Decimal
Convert 2/3 to a decimal.
Solution
To convert 2/3 to a decimal, follow these steps:
Step 1: Identify the numerator and denominator
From the question, the numerator is 2, and the denominator is 3
Step 2: Divide the numerator by the denominator using the long division method
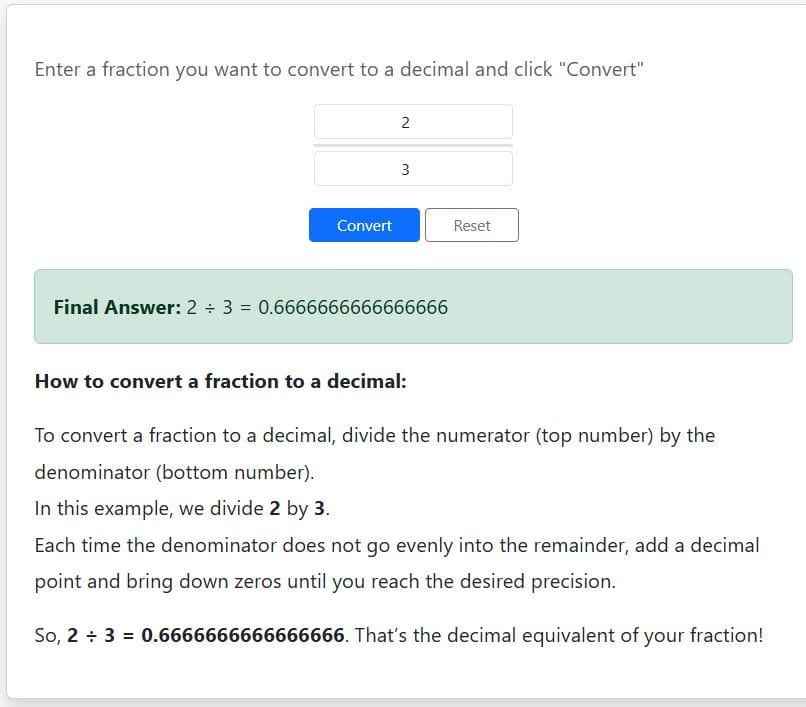
Using the long division method, 2÷3 = 0.666…
From the solution, the digit 6 keeps repeating without an end. This is called a repeating/recurring decimal.
Alternatively, using the online fraction-decimal calculator instantly gives you the recurring decimal as shown below:
Quick Tip to Remember
- If the division ends, you get a terminating decimal.
- If the same digit(s) repeat, use a bar to show the repeating part.
- For mixed numbers, convert only the fraction and then add it to the whole number.
- If the fraction looks complicated, simplify it first before dividing. It saves time and effort.
Fraction to Decimal Worksheet
Many fractions are used so often that it helps to remember their decimal forms. The following fraction-decimal worksheet shows the decimal equivalent of the most commonly used fractions.
| Fraction | Decimal Equivalent | Notes |
|---|---|---|
| 1/2 | 0.5 | Exact |
| 1/3 | 0.333… | Repeating decimal |
| 2/3 | 0.666… | Repeating decimal |
| 1/4 | 0.25 | Exact |
| 3/4 | 0.75 | Exact |
| 1/5 | 0.2 | Exact |
| 2/5 | 0.4 | Exact |
| 3/5 | 0.6 | Exact |
| 4/5 | 0.8 | Exact |
| 1/6 | 0.166… | Repeating decimal |
| 5/6 | 0.833… | Repeating decimal |
| 1/8 | 0.125 | Exact |
| 3/8 | 0.375 | Exact |
| 5/8 | 0.625 | Exact |
| 7/8 | 0.875 | Exact |
| 1/10 | 0.1 | Exact |
| 9/10 | 0.9 | Exact |