Improper to Mixed Fraction Calculator
Easily Convert Improper Fractions to Mixed Numbers in Seconds. Our Improper to Mixed Fraction Calculator makes it easy to convert any improper fraction into a mixed number in seconds. Simply enter your numerator and denominator, and the tool will instantly show the final answer along with a clear step-by-step solution. Perfect for students, teachers, or anyone looking for a quick improper to mixed fraction converter.
Related Calculators
How to Use the Improper to Mixed Fraction Calculator
Using our Improper to Mixed Fraction Calculator is quick and straightforward. Follow these simple steps:
- Enter the Numerator and Denominator
- Type the top number (numerator) and the bottom number (denominator) of your fraction into the input boxes.
- Click the Convert Button
- Once you enter your values, press Convert to instantly see the mixed fraction.
- View the Answer and Step-by-Step Solution
- The calculator will first display the final answer, then show you a clear, step-by-step explanation of how the result was obtained.
- Use Reset for New Calculations
- If you want to try another fraction, simply click the Reset button to clear the fields and start fresh.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. In other words, the top number is not smaller than the bottom number. For example, fractions like $\tfrac{7}{4}$, $\tfrac{9}{5}$, and even $\tfrac{12}{12}$ are all considered improper fractions. Notice that when the numerator equals the denominator, such as in $\tfrac{3}{3}$ or $\tfrac{9}{9}$, the fraction is still classified as improper, but it simplifies neatly into the whole number 1. Similarly, $\tfrac{9}{3}$ simplifies into the whole number 3.
On the other hand, when the numerator is smaller than the denominator, the fraction is called a proper fraction. For instance, $\tfrac{3}{5}$ or $\tfrac{2}{7}$ are proper fractions because the numerator is less than the denominator. Therefore, the key difference between improper and proper fractions is the relationship between the numerator and denominator. Notably, improper fractions are greater than or equal to one whole, while proper fractions are always less than one whole.
What is a Mixed Fraction?
A mixed fraction is a number that combines a whole number with a proper fraction. In other words, it shows both how many whole parts there are and the fraction that remains. For example, $2 \tfrac{1}{3}$, $4 \tfrac{3}{5}$, and $7 \tfrac{2}{9}$ are all mixed fractions because each includes a whole number and a proper fraction side by side.
Mixed fractions are often easier to understand than improper fractions because they show the quantity in a more natural way. For instance, saying $2 \tfrac{1}{3}$ is usually clearer than saying $\tfrac{7}{3}$. This is especially useful when dealing with real-life contexts like measuring lengths, cooking, or dividing objects. This explains why mixed fractions are commonly used in everyday situations and teaching.
How to Convert Improper Fractions to Mixed Fractions (Step-by-Step)
Converting an improper fraction into a mixed fraction is a simple process. To change an improper fraction into a mixed number, follow these steps:
- Divide the numerator by the denominator. The quotient will be the whole number part of the mixed fraction.
- Write down the remainder. This remainder becomes the numerator of the fraction part.
- Keep the same denominator. The denominator remains unchanged.
- Combine the whole number and the fraction. This gives you the mixed fraction.
Worked Examples
Example 1:
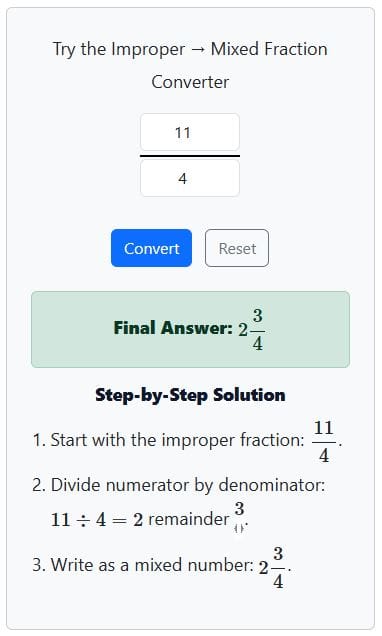
$\tfrac{11}{4} = 2 \tfrac{3}{4}$
Here, 11 ÷ 4 = 2 remainder 3. The whole number is 2 and the fraction part is 3/4.
Hence, the mixed fraction becomes $2 \tfrac{3}{4}$
Example 2:
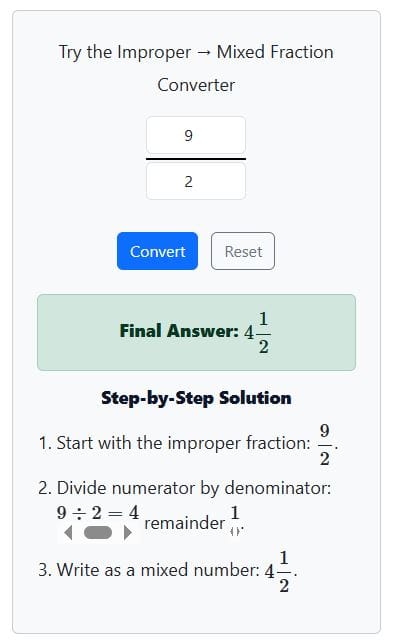
$\tfrac{9}{2} = 4 \tfrac{1}{2}$
In this case, 9÷2=4 remainder 1. Thus, the whole number is 4, and the fraction is 1/2
Hence, the mixed fraction becomes $4 \tfrac{1}{2}$
Frequently Asked Questions
An improper fraction is a fraction where the numerator (top number) is greater than or equal to the denominator (bottom number). For example, $\tfrac{7}{4}$, $\tfrac{12}{12}$, and $\tfrac{9}{3}$ are improper fractions because the numerator is not less than the denominator.
A mixed fraction, or mixed number, is a number made up of a whole number plus a proper fraction. It looks like $2 \tfrac{1}{3}$ or $5 \tfrac{4}{7}$. The proper fraction part always has its numerator smaller than its denominator.
Here’s the manual method for converting any improper fraction to mixed fraction:
– Divide the numerator by the denominator.
– The quotient becomes the whole number.
– The remainder becomes the numerator of the fraction part.
– Use the same denominator.
No — a proper fraction is already in the simplest form in terms of mixed vs improper. It has numerator < denominator. With no whole number part, it is less than 1. Therefore, a “proper fraction” doesn’t convert into a mixed number since it doesn’t produce a whole number + fraction.
To write an improper fraction as a mixed fraction, first divide the numerator by the denominator. The whole number part of the quotient becomes the whole number in the mixed fraction, while the remainder becomes the new numerator placed over the original denominator. Finally, if the fractional part can be simplified, reduce it to lowest terms. For example,
$\dfrac{14}{6} = 2 \dfrac{2}{6} = 2 \dfrac{1}{3}$.