Binomial Distribution Calculator

This calculator finds the exact and cumulative probabilities from a binomial distribution. It also produces a probability mass function (PMF) to help you compute any cumulative probability manually.

How to Use the Binomial Probability Calculator

To compute binomial probabilities using the calculator, you only need to:

1. Enter the number of trials (n)
2. Enter the probability of success (p)
3. Enter the number of successes (x)
4. Click the “Calculate” button

The calculator will instantly compute the following probabilities:

• The exact probability that the random variable X is exactly equal to a specified value x, P(X=x).
• The cumulative probability that the random variable X takes a value less than x, P(X<x).
• The cumulative probability that the random variable X takes a value less than or equal to x, P(X≤x).
• The cumulative probability that the random variable X takes a value greater than x, P(X>x).
• The cumulative probability that the random variable X takes a value greater than or equal to x, P(X≥x).

It will also display the mean and standard deviation of the binomial experiment, as well as a PMF table showing P(X = x) for all possible outcomes.

What is a Binomial Distribution?

A binomial distribution is a probability distribution that describes the likelihood of obtaining a fixed number of successes (x) in a specified number of independent trials (n), where each trial has only two possible outcomes (success or failure) and the probability of success remains constant across trials.

Therefore, to use a binomial distribution, the following conditions must be met:

• The number of trials is fixed.
• Each trial is independent of the others.
• Each trial has only two possible outcomes: success or failure.
• The probability of success is the same for every trial.

Binomial Distribution Formula

The binomial distribution formula is used to calculate the probability of obtaining exactly x successes in n independent trials when the probability of success is constant.

The formula is:

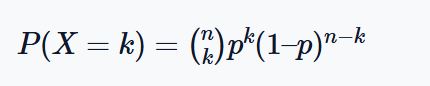
Where:

• n is the total number of trials
• k is the number of successes
• p is the probability of success in a single trial
• (1 – p) is the probability of failure in a single trial

Struggling with computing binomial probabilities by hand? Check out our complete guide on how to use the binomial formula to compute probabilities.

How to Compute Binomial Probabilities using the Calculator [With Examples]

Want to learn how to use the binomial calculator to find exact and cumulative probabilities? Check out the following examples that show you exactly how to find all the possible exact and cumulative probabilities using the calculator.

Scenario: A manufacturer knows that 3% of its bulbs are defective. An inspector tests 20 bulbs. Let X be the number of defective bulbs. Using the calculator, compute the following probabilities:

1. Probability that exactly 2 bulbs are defective
2. Probability that at most 2 bulbs are defective
3. Probability that fewer than 2 bulbs are defective
4. Probability that at least 3 bulbs are defective
5. Probability that more than 1 bulb is defective

1) Finding Exact Probability, P(X=k)

i) Find the probability that exactly 2 bulbs are defective

To find the probability of getting exactly 2 defective bulbs using the calculator, follow these steps:

1. Enter the number of trials (n) = 20
2. Enter the probability of success (p) = 0.03
3. Enter x = 2
4. Look for P(X = 2) in the calculator results

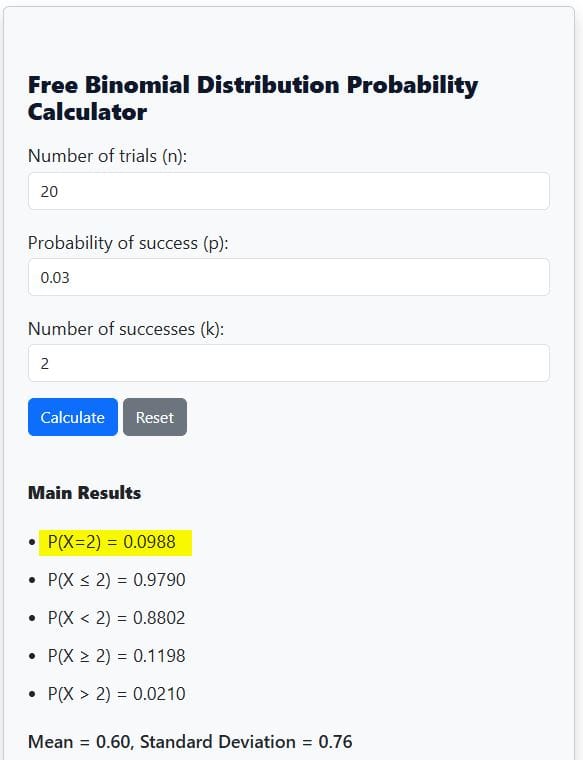
From the calculator output, P(X = 2) = 0.0988 (See Figure 1). This means there is about a 9.88% chance of finding exactly 2 defective bulbs.

2) Finding Cumulative Probability, P(X≤k)

ii) Find the probability that at most 2 bulbs are defective?

To find the probability that at most 2 defective bulbs are found (0, 1, or 2), follow these steps:

1. Enter the number of trials (n) = 20
2. Enter the probability of success (p) = 0.03
3. Enter x = 2
4. Look for P(X ≤ 2) in the calculator results.

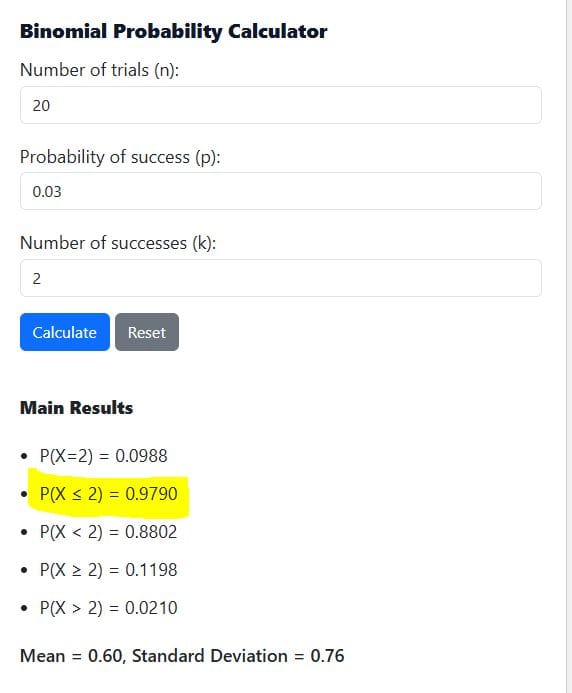
From the calculator output, P(X ≤ 2) = 0.9790 (See Figure 2). This implies that there is a 97.9% chance that the inspector finds at most 2 defective bulbs.

3) Find Cumulative Probability, P(X<k)

iii) Find the probability that fewer than 2 bulbs are defective?

To find the probability that the inspector finds fewer than 2 defective bulbs (either 0 or 1), follow these steps:

1. Enter the number of trials (n) = 20
2. Enter the probability of success (p) = 0.03
3. Enter x = 2
4. Look for P(X < 2) in the calculator results

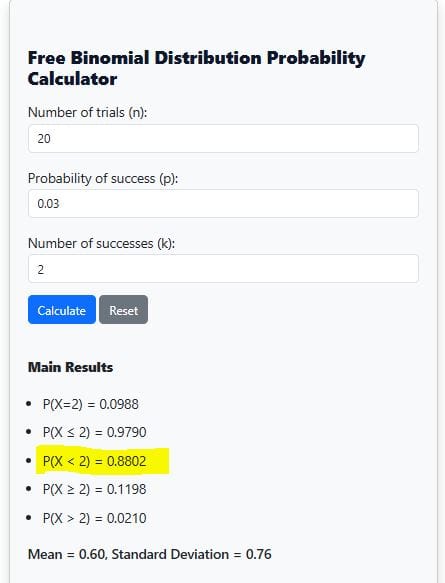
From the calculator output, P(X < 2) = 0.8802 (See Figure 3). This means that there is an 88.02% chance of finding fewer than 2 defective bulbs.

4) Find Cumulative Probability, P(X≥k)

iv) Find the probability that at least 3 bulbs are defective?

To find the probability of getting 3 or more defective bulbs, follow these steps:

1. Enter the number of trials (n) = 20
2. Enter the probability of success (p) = 0.03
3. Enter x = 3
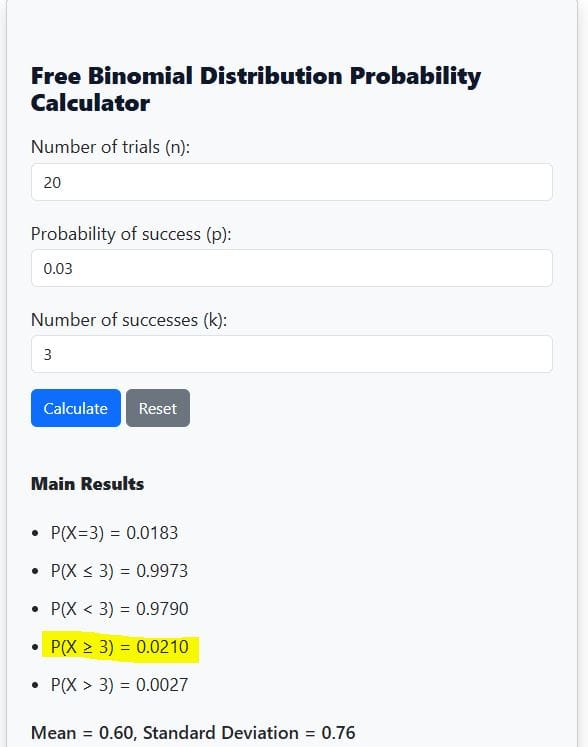
4. Look for P(X ≥ 3) in the calculator results

From the calculator output, P(X ≥ 3) = 0.0210 (See Figure 4). This suggests that there is about a 2.10% chance of finding 3 or more defective bulbs in the sample.

5) Find Cumulative Probability, P(X>k)

v) Find the probability that more than 1 bulb is defective?

To find the probability of getting one or more defective bulbs, follow these steps:

1. Enter the number of trials (n) = 20
2. Enter the probability of success (p) = 0.03
3. Enter x = 1
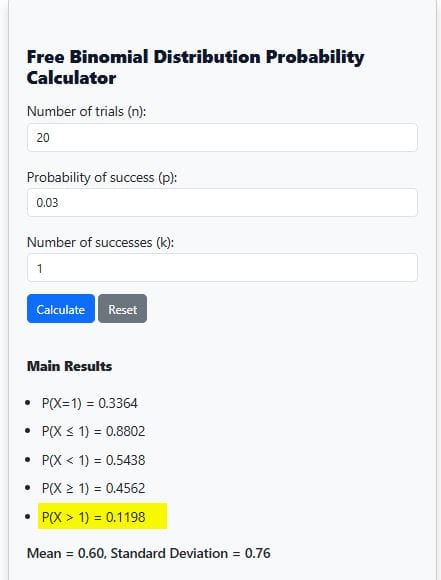
4. Look for P(X > 1) in the calculator results

From the calculator output, P(X > 1) = 0.1198 (See Figure 5). This suggests that there is about a 11.98% chance of finding one or more defective bulbs in the sample.

Frequently Asked Questions