Cochran’s formula: Definition, Calculation, When to Use it & Mistakes to Avoid

When writing the methodology section of a quantitative research study, you may need to determine the appropriate sample size. While searching for the best sample size formula, you might come across Cochran’s formula. This formula makes it easy to calculate the ideal number of participants needed for accurate results. It also ensures your study is reliable without wasting time or resources on too many or too few respondents. Cochran’s formula is especially useful for surveys, polls, and research projects where precision matters. In this article, we will explain what Cochran’s formula is, show how to compute sample size step by step, and highlight common mistakes to avoid.

Definition

Cochran’s formula is a statistical method used to calculate the ideal sample size for a study or survey. It helps researchers determine how many participants they need to produce reliable and accurate results. By using this formula, you can avoid having too few respondents, which may make your study less reliable, or too many, which can waste time and resources.

This formula is commonly used when working with large populations, especially in surveys, polls, and research projects that involve categorical data. It is particularly useful when you want to estimate proportions and ensure that your findings are statistically valid.

Cochran’s Formula Explained

Cochran’s formula is a sample size determination formula that was developed by William Cochran in 1977 to help researchers calculate the ideal sample size for surveys and research studies. Thus, it help researchers determine the minimum number of participants/item required to achieve reliable and accurate results. In other words, Cochran’s formula ensures that the sample is representative of the target population without adding unnecessary costs or effort during data collection.

The formula is based on three key parameters: the desired confidence level, the margin of error (precision), and the estimated proportion (p) of the population. Cochran’s 1977 proposed two key variations of the formula:

1. Assuming Infinite population
2. Assuming a finite population (You know the population size).

Each of these formula is discussed below:

1. Cochran’s Formula for Infinite Population

In sampling, an infinite population refers to a population so large or continuously generated; that its exact size cannot be determined. Because of this, selecting a sample from such a population does not meaningfully change the overall pool of individuals or items. In contrast, finite populations have a known, countable number of elements (N).

To ensure that researchers can still estimate an appropriate sample size when the population is extremely large or unknown, Cochran proposed a formula specifically for infinite populations. This formula helps capture the variability within a very large population while maintaining a desired level of accuracy.

The Cochran’s sample size formula for an infinite population is:

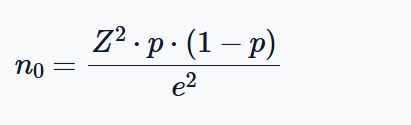
Where:

• n0 is the required sample size (for infinite population)
• Z is the Z-value corresponding to the desired confidence level (e.g., 1.96 for 95%)
• p is the estimated proportion of the population (use 0.5 if unknown)
• e is the desired margin of error (in decimal form, e.g., 0.05 for 5%)

Note. You should only use this formula when the population is too large to count, such as in nationwide surveys.

2. Cochran’s Formula for Finite Population

Unlike infinite populations, a finite population has a fixed, countable number of elements (N). When sampling from such a population, each selected unit slightly reduces the pool of remaining units. This means that the variability within the population changes as you draw more samples — an effect that must be corrected for to avoid overestimating the required sample size.

To address this, Cochran introduced a finite population correction (FPC) that adjusts the initial sample size (n₀) calculated using the infinite-population formula. This adjustment ensures that the sample size remains accurate and efficient when the total population is relatively small.

The adjusted Cochran’s formula for finite populations is:

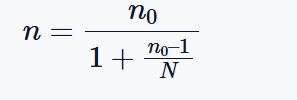
Where:

• n = adjusted sample size
• n₀ = initial sample size from Cochran’s formula
• N = total population size

This adjustment ensures your sample size accurately reflects smaller populations without overestimating the number of respondents needed.

Tip: The Cochran’s formula for a finite population requires you to first calculate the sample size using the infinite formula. Then you need to use the resulting value to determine the adjusted sample size for your actual population.

Sample Size Determination using Cochran’s Formulas (Examples)

Below are clear, worked examples that show how to apply Cochran’s formulas step-by-step. You’ll learn how to apply both the infinite-population formula (to get $n_0$​) and the finite-population correction (to get n). You’ll also learn how to adjust for nonresponse.

Example 1: Infinite Population

Imagine you work for a national research organization and you want to find out what proportion of adults prefer online shopping over in-store shopping. Since the adult population in the country is extremely large (effectively “infinite” for sampling purposes), Cochran’s infinite population formula is appropriate.

You want your survey to meet the following conditions:

• Confidence level: 95% (Z = 1.96)
• Estimated proportion (p): 0.5 (since you don’t have prior data)
• Margin of error: 0.05 (±5%)

Note. A z-score of 1.96 is obtained by looking up the value from the standard normal tables. Looking up for (1-0.05/2) = 0.975 from the tables will give you 1.96

Therefore, to calculate the minimum sample size assuming an infinite population, you can follow these steps:

• Step 1: Write the Formula

$$n_0 = \frac{Z^2 \cdot p \cdot (1 – p)}{e^2}$$

• Step 2: Substitute the values

$$n_0 = \frac{1.96^2 \cdot 0.5 \cdot 0.5}{0.05^2}$$

• Step 3: Calculate both the numerator and denominator and solve for n0. This gives:

$$n_0 = \frac{0.9604}{0.0025} = 384.16$$

• Step 4: Round up the result

Since sample sizes must be whole numbers and rounding up protects your margin of error, the rounded up sample size becomes 385 respondents.

Therefore, you’ll need at least 385 completed surveys to estimate the proportion of adults who prefer online shopping with 95% confidence and ±5% margin of error.

Bonus: Adjusting for nonresponse (recommended in real surveys)

In real-world surveys, not everyone responds. Let’s say you expect an 80% response rate. You can easily adjust for this nonresponse by dividing the sample size by the anticipated response rate.

Thus,

$$\text{Invites needed} = \frac{385}{0.8} = 481.25$$

Rounding up to the nearest whole number, we have 482 people. This way, you’ll still end up with around 385 complete responses after accounting for nonresponse.

Example 2: Finite Population

In Example 1, we calculated the initial (infinite population) sample size as: n0​=384.16(rounded up to 385)

Now let’s see how this changes when the population is not infinite but a known, limited group.

Suppose you now want to survey all registered high school teachers in a county to find out whether they support a new teaching policy. The county has exactly N = 2,000 teachers.

Because the population is known and not very large, we must apply Cochran’s Finite Population Correction (FPC) to adjust the sample size downward.

Now, assuming the survey requirements remain the same as in example 1, then we can apply the finite population correction factor as follows:

• Step 1: Apply the Finite Population Correction Formula

$$n = \frac{n_0}{1 + \frac{n_0 – 1}{N}}$$

• Step 2. Substitute the values in the formula

$$n = \frac{384.16}{1 + \frac{384.16 – 1}{2000}}$$

• Step 3: Solving the numerator and denominator, we have: n = 322.50

• Step 4: Rounding up to the nearest whole number, n = 323 teachers.

Because your total population is only 2,000 teachers, you don’t need as many respondents as you would in an infinite or very large population. The finite population correction reduced the required sample from 385 down to 323, while still maintaining 95% confidence and ±5% margin of error.

Optional: Adjust for nonresponse

If you expect, say, an 80% response rate, then you can adjust for the nonresponse by dividing the sample size by the response rate.

Thus,

$$\text{Invites needed} = \frac{323}{0.80} = 403.75 \Rightarrow \textbf{invite 404 teachers}$$

This means, with an 80% response rate, you’ll need to invite about 404 teachers to achieve about 323 participants.

When to Use Cochran’s Sample Size Formula

Cochran’s formula is a powerful tool for calculating sample size. However, it works best under certain conditions. Thus, before using the formula, make sure that these conditions are met for accurate and meaningful results.

1. Large or Known Population: Cochran’s formula is most suitable when the population is large (approaching infinity) or when the total population size (N) is known.
2. Random Sampling: The data should come from a random sample where every individual in the population has an equal chance of inclusion. This helps to reduce bias and improve accuracy.
3. Proportion Data (Yes/No, Success/Failure): The formula is mainly used for estimating proportions in the population. For example, the proportion of people who support a policy or the percentage of customers satisfied with a product.
4. Desired Confidence Level and Margin of Error: You must define the confidence level (such as 90%, 95%, or 99%) and the acceptable margin of error (e.g., 0.05). These values determine how precise and reliable your results will be.
5. Sufficiently Large Population Size: If your population is too small (less than 30), Cochran’s formula may not be suitable. In such cases, other sample size calculation methods may provide better accuracy.
6. Estimated Population Proportion (p): You need to have an estimate of the population proportion (p). If it is unknown, using 0.5 gives the most conservative and largest sample size estimate.

Tip: You should use the Cochran’s sample size formula for surveys and studies that involve large populations, random sampling, and proportion-based data.

Common Mistakes When Using Cochran’s Formula

It is easy to make small errors when calculating sample size, and these mistakes can lead to inaccurate results. Here are some common issues to watch out for:

• Assuming p=0.5 without justification. While 0.5 is a safe default, you should use a more accurate estimate if you have prior information about the population.
• Using the wrong Z-score for the confidence level. Always match your confidence level with the correct Z-value. For example, 95% uses 1.96.
• Not adjusting for a finite population when necessary. If your population is small or known, you must apply the finite population correction; otherwise, your sample size may be too large.

Conclusion

Cochran’s formula is a reliable way to determine the ideal sample size for your study. It helps ensure your results are accurate while saving time and resources. Whether your population is large or small, using the correct formula is essential for valid research. To make the process even easier, you can use our Cochran’s Formula Calculator. This tool not only calculates the sample size for both finite and infinite populations but also provides a step-by-step solution, showing exactly how the sample size is computed. Try it to plan your study with confidence and accuracy.

Frequently Asked Questions