This calculator computes the minimum sample size for your study or survey using Cochran’s formula. It automatically applies the appropriate formula based on your input:
- For an unknown or infinitely large population, the calculator uses the standard Cochran’s formula for infinite populations.
- For a finite and known population, it applies the finite population correction (FPC) to compute the adjusted sample size.
In addition to providing the minimum sample size, the calculator also gives a step-by-step solution of how the sample size was calculated, making it easy to understand and apply for your research.
How to Use the Cochran’s Formula Calculator
To determine the minimum sample size for your survey/study using the calculator, follow these steps:
- Enter your confidence level (%). This represents how certain you want to be that your sample accurately reflects the population. Common values are 90%, 95%, or 99%.
- Enter your margin of error (e). This indicates the amount of error you are willing to tolerate in your results. You only need to enter this value as a decimal. For instance, for 5% margin of error, you need to enter 0.05.
- Enter your estimated proportion (p). This is your best estimate of the population proportion. If you are unsure, use 0.5 (50%) to ensure the maximum sample size and the most conservative estimate.
- Enter the population size (N) (optional). If you know your total population, enter it here. If not, you can leave it blank. The calculator will assume an infinite population.
- Click the “Calculate” button: The calculator instantly computes the minimum sample size for your study.
Note. In addition to the minimum sample size, the calculator provides you with a clear solution to help you learn how to find the sample size (n) manually.
Cochran’s Sample Size Formula
Cochran’s formula was developed by William G. Cochran in 1977 to help researchers determine the minimum sample size for a desired level of precision. It is ideal when you want to determine the minimum sample size for large, infinite, or unknown populations, particularly for categorical data and proportion-based surveys
The formula is n₀ = Z²·p(1–p)/e²
Where:
- n₀ is the minimum sample size you wish to estimate
- e is the desired level of precision (margin of error)
- p is the population proportion with the characteristics of interest
- z is the z-value corresponding to your preferred confidence level. For instance, 1.96 for 95% confidence level.
Example
A national research organization intends to conduct a survey to estimate the proportion of adults in the country who prefer online shopping over in-store shopping. Because the adult population is extremely large, it can be treated as effectively infinite.
The researchers want the survey results to be 95% reliable, and they require the estimated proportion to be within five percentage points of the true population value. Since no prior information is available about adults’ shopping preferences, a conservative approach is adopted when planning the study. Compute the minimum sample size required for this survey.
Solution
From the question, we know that:
- Margin of error, e = 5% = 0.05
- The population is infinite (large and unknown)
- We want to be 95% confident.
- We need to use a conservative proportion of 0.5 since no prior information is available on adults’ shopping preferences.
To compute the minimum sample size, we should use Cochran’s formula.
Given a 95% confidence level, the corresponding z-critical value is 1.96. Thus, the z-value to use in the Cochran’s formula is z=1.96.
Want to learn how to find the z-value given a confidence level? Check out our guide on how to find the z-critical value from z-tables.
Now, to compute the minimum sample size, we substitute the values into Cochran’s sample size formula. This gives:
n₀ = 1.96²·0.5(1–0.5)/0.05²
= 0.9604/0.0025
= 384.16
Rounding up to the nearest whole number gives n₀ = 385
Therefore, the minimum sample size for the survey is 385 participants.
Adjusting for Finite Population Correction (FPC)
Unlike an infinite population, a finite population has a fixed, countable number of elements (N). When sampling from such a population, selecting one unit from the population reduces the pool of the remaining units. In other words, the variability within the population changes as you draw more samples.
To avoid overestimating the sample size, the variability within the population must be corrected. In this case, we use the finite population correction (FPC) factor to adjust the initial sample size (n₀) calculated using Cochran’s formula. This adjustment ensures that the sample size remains accurate and efficient when the total population is relatively small.
The finite population correction formula is n = n₀ / [1 + ((n₀–1)/N)]
Where:
- n₀ is the initial sample size computed from Cochran’s formula
- N is the known/finite population
- n is the adjusted sample size for the finite population
Example
Assume the organization now wants to conduct the same survey among employees of a large corporation with a known total workforce of 8,000 adults. Since the population size is known and finite, the initial sample size calculated using Cochran’s formula must be adjusted using the finite population correction.
Here’s how we can adjust for the sample size using the FPC.
We now know that N = 8000
From the previous example, n₀ = 384.16
Applying the FPC formula, we have:
n = 384.16 / [1 + ((384.16–1)/8000)]
=384.16/[1+0.047895]
=366.60
Rounding up to the nearest whole number gives n = 367.
Therefore, for a total workforce of 8000, the organization will need to survey 367 participants.
Tip: You should use the Cochran’s sample size formula for surveys and studies that involve large populations, random sampling, and proportion-based data.
How to Determine Sample Size Using the Cochran’s Calculator: Examples
Example 1. Let’s say you want to determine the sample size for a survey with the following conditions:
- Confidence level = 95% (Z = 1.96).
- Proportion (p) = 0.5
- Margin of error (e) = 0.05
To compute the sample size using the calculator, follow these steps:
- Insert 95 in the confidence level input section
- Insert margin of error 0.05
- Specify the proportion as 0.5
- Click the Calculate button
The calculator will give you the minimum sample size after rounding up as 385 (Figure 1).
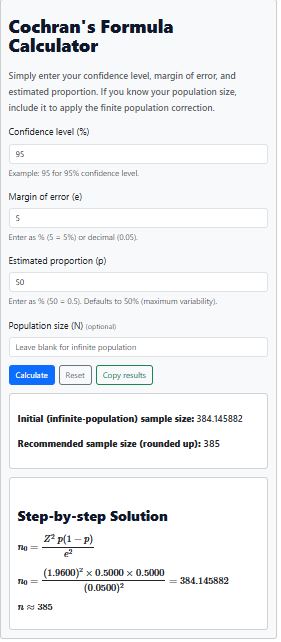
Example 2. Assuming the parameters remain the same as in example 1 (i.e., 95% confidence, p = 0.5, margin of error = 5%). Suppose now that the actual population size is known to be 1,000 people.
The calculator can adjust for the finite population correction for you. You simply need to specify the known population in the “Population size (N) (optional)” section and click the Calculate button.
The calculator will calculate and round up the adjusted sample size for you. The resulting sample size for 1000 people will be 278 participants (Figure 2).
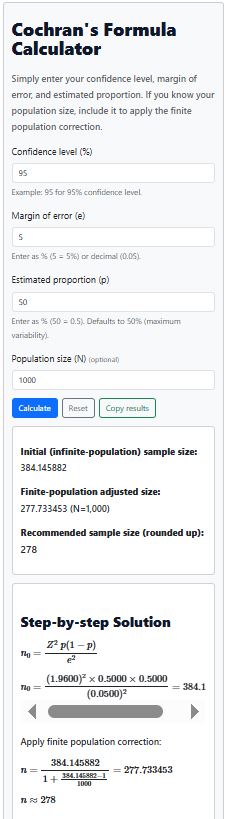
Common Mistakes When Using Cochran’s Formula
It is easy to make small errors when calculating sample size using Cochran’s formula. These mistakes can lead to inaccurate results and unreliable findings. Here are some common mistakes you should avoid:
- Assuming p = 0.5 without justification. While 0.5 is a safe default, you should use a more accurate estimate if you have prior information about the population.
- Using the wrong Z-score for the confidence level. Always match your confidence level with the correct Z-value. For example, 95% uses 1.96.
- Not adjusting for a finite population when necessary. If your population is small or known, you must apply the finite population correction; otherwise, your sample size may be too large.